
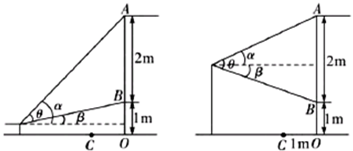
 ���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ����
���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ����| �� |
| 2 |
| ||||
1+
|
| 2 | ||
x+
|
| (1-a)(3-a) |
| x |
| (1-a)(3-a) |
| (1-a)(3a) |
| (1-a)(3-a) |
| 2 |
| (1-a)(3-a) |
| 2 |
| (1-a)(3-a) |
| 2 |
| x |
| ||||
1-
|
| 2 | ||
x-
|
| (a-1)(3-a) |
| x |
| 2 |
| 2 |
| (1-a)(3-a) |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������ѧ2011-2012ѧ��߶���ѧ�����п�����ѧ�������� ���ͣ�044
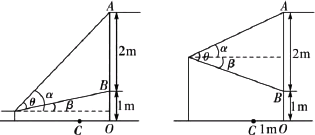
���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa��(0��a��3)�����ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽ�![]() ���
���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
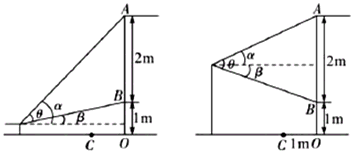 ���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ����
���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
(1)�����ĸ��ʷֲ�����ѧ����;
(2)�ǡ�����f(x)=x2-2��x�����䣨-��,2���ϵ����ݼ���Ϊ�¼�m,��P(m).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��1����εĸ��ʹ�������ѧ������
��2���ǡ�����f(x)=x2-2��x�����䣨-��,2���ϵ����ݼ���Ϊ�¼�M����P��M��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com