
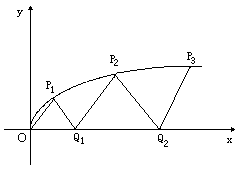
如图,曲线y2=x(y≥0)上的点Pi与x轴的正半轴上的点Qi及原点O构成一系列正三角形:△OP1Q1,△Q1P2Q2,…,△Qn-1PnQn,….设正三角形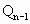 PnQn的边长为an,n∈N*(记Q0为O),Qn(Sn,0).
PnQn的边长为an,n∈N*(记Q0为O),Qn(Sn,0).
(1)求a1的值;
(2)求数列{an}的通项公式an;
(3)求证:当n≥2时,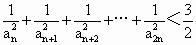 .
.
|
解 (1)由条件可得P1(
(2)∵Sn=a1+a2+…+an, ∴点Pn+1(Sn+ Sn= 于是当n≥2,n∈N*时,an=Sn-Sn-1=( 即 ∵an+1>an>0,∴an+1-an= 又当n=1时,S1= ∴a2-a1= 所以数列{an}是首项为 (3)由(2)得an=
欲证 设f(n)=4n2-7n-3,当n≥ 所以只需验证n=2时不等式成立.事实上, 综上所述,原不等式成立. |


科目:高中数学 来源:学习周报 数学 人教课标高二版(A选修1-1) 2009-2010学年 第25期 总第181期 人教课标版(A选修1-1) 题型:013
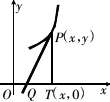
如图,曲线y=f(x)上任一点P的切线PQ交x轴于Q,过P作PT垂直于x轴于T,若△PTQ的面积为![]() ,则y与
,则y与![]() 的关系满足
的关系满足
y=![]()
y=-![]()
y=![]()
y2=![]()
查看答案和解析>>
科目:高中数学 来源:福建省泉州市普通中学2012届高中毕业班质量检查数学理科试题 题型:013
函数的图象与方程的曲线有着密切的联系,如把抛物线y2=x的图象绕原点沿逆时针方向旋转90°就得到函数y=x2的图象.若把双曲线![]() -y2=1绕原点按逆时针方向旋转一定角度
-y2=1绕原点按逆时针方向旋转一定角度![]() 后,能得到某一个函数的图象,则旋转角
后,能得到某一个函数的图象,则旋转角![]() 可以是
可以是
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试、数学理科(安徽卷) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:河南省平顶山新乡许昌市2009-2010学年高三第三次调研考试理科数学试题 题型:044
如图,点An(xn,yn)是曲线y2=2x(y≥0)上的点,点Bn(an,0)是x轴上的点,△Bn-1AnBn是以An为直角顶点的等腰直角三角形,其中n=1,2,3,…,B0为坐标原点.
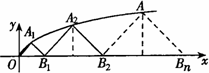
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列bn=2n-1,求最小正整数m,使得对任意的n∈N*,当n>m时,an<bn成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com