
 半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.
半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径. 的两部分的比
的两部分的比 :
: =1:2时,求D点到平面ABC的距离.
=1:2时,求D点到平面ABC的距离.
 .
. BD•CD≤
BD•CD≤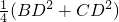 =
=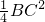 =12(当且仅当BD=CD时取“=”)
=12(当且仅当BD=CD时取“=”)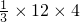 =16;
=16; ,CD=6.
,CD=6. =
= ,
, .
.

科目:高中数学 来源: 题型:
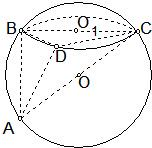 半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.
半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.查看答案和解析>>
科目:高中数学 来源: 题型:
 半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径.
半径为R的球O的截面BCD把球面面积分为两部分,截面圆O1的面积为12π,2OO1=R,BC是截面圆O1的直径,D是圆O1上不同于B,C的一点,CA是球O的一条直径. |
| BC |
 |
| BD |
 |
| DC |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市启恩中学高三数学专题练习:立体几何(文科)(解析版) 题型:解答题
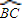 的两部分的比
的两部分的比 :
: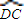 =1:2时,求D点到平面ABC的距离.
=1:2时,求D点到平面ABC的距离.
查看答案和解析>>
科目:高中数学 来源:2007年高考数学模拟试卷(解析版) 题型:解答题
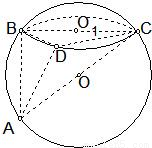
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com