
【题目】若学生![]() 一天学习数学超过两个小时的概率为
一天学习数学超过两个小时的概率为![]() (每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(Ⅰ)①设学生![]() 本周一天学习数学超过两个小时的天数为
本周一天学习数学超过两个小时的天数为![]() 求
求![]() 的分布列与数学期望
的分布列与数学期望![]()
②求学生![]() 本周数学学习投入的概率.
本周数学学习投入的概率.
(Ⅱ)为了研究学生学习数学的投入程度和本周数学周练成绩的关系,随机在年级中抽取了![]() 名学生进行调查,所得数据如下表所示:
名学生进行调查,所得数据如下表所示:
成绩理想 | 成绩不太理想 | 合计 | |
数学学习投入 | 20 | 10 | 30 |
数学学习不太投入 | 10 | 15 | 25 |
合计 | 30 | 25 | 55 |
根据上述数据能否有![]() 的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
附:![]()
|
|
|
|
|
|
|
|
|
|
| 10.828 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点坐标为![]() ,且短轴一顶点
,且短轴一顶点![]() 满足
满足![]() .
.
(1)求椭圆的方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为15°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值为 . 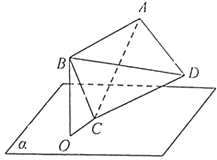
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣ax+a+3,g(x)=ax﹣2a.
(1)若函数h(x)=f(x)﹣g(x)在[﹣2,0]上有两个零点,求实数a的取值范围;
(2)若存在x0∈R,使得f(x0)≤0与g(x0)≤0同时成立,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且定义域为
,且定义域为![]() .
.
(1)求关于![]() 的方程
的方程![]() 在
在![]() 上的解;
上的解;
(2)若![]() 在区间
在区间![]() 上单调减函数,求实数
上单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的实根,求实数
上有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg![]() ,
,
(1)求f(x)的定义域并判断它的奇偶性.
(2)判断f(x)的单调性并用定义证明.
(3)解关于x的不等式f(x)+f(2x2﹣1)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com