分析:(Ⅰ)求导函数,求得曲线在点Q
0处的切线方程,令y=0,可求x
1;
(Ⅱ)曲线在点
Qn-1(xn-1,)处的切线方程为
y-=2xn-1(x-xn-1),令y=0,得
x=xn-1,即
xn=xn-1,从而可得{x
n}是以
x1=为首项,
为公比的等比数列,由此可求x
n;
(Ⅲ)由(Ⅱ)得
an==n•2n,所以
Sn=1×2+2×22+3×23+…+n×2n,利用错位相减法可求数列{a
n}的前n项的和S
n.
解答:解:(Ⅰ)因为y'=2x,所以曲线在点Q
0处的切线方程为y-1=2(x-1).
令y=0,得
x=,即
x1=.
(Ⅱ)曲线在点
Qn-1(xn-1,)处的切线方程为
y-=2xn-1(x-xn-1).
令y=0,得
x=xn-1,即
xn=xn-1.
所以{x
n}是以
x1=为首项,
为公比的等比数列.
所以
xn=×()n-1=.
(Ⅲ)由(Ⅱ)得
an==n•2n.
∴
Sn=1×2+2×22+3×23+…+n×2n①
∴
2Sn=1×22+2×23+…+(n-1)×2n+n×2n+1②
由①-②得,
-Sn=2+22+23+…+2n-n×2n+1=
-n•2n+1=(1-n)•2n+1-2.
∴
Sn=(n-1)•2n+1+2.
点评:本题考查导数的几何意义,考查等比数列的判定,考查等比数列的通项,考查错位相减法求数列的和,属于中档题.



 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案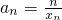 ,求数列{an}的前n项的和Sn.
,求数列{an}的前n项的和Sn.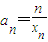 ,求数列{an}的前n项的和Sn.
,求数列{an}的前n项的和Sn.