
解:(1)取BC中点G点,连接AG,FG,如图1
因为AE⊥面ABC,BD∥AE,所以BD⊥面ABC.
又AG?面ABC,所以BD⊥AG.
又AC=AB,G是BC的中点,所以AG⊥BC,所以AG⊥平面BCD.
又因为F是CD的中点且BD=2,所以FG∥BD且FG=1,所以FG∥AE.
又AE=1,所以AE=FG,所以四边形AEFG是平行四边形,所以EF∥AG,所以EF⊥面BCD
(2)设AB中点为H,则由AC=AB=BC=2,可得CH⊥AB且CH=

,如图2
又BD∥AE,所以BD与AE共面.
又AE⊥面ABC,所以平面ABDE⊥平面ABC.
所以CH⊥平面ABDE,即CH为四棱锥C-ABDE的高.
故四棱锥C-ABDE的体积为V
C-ABDE=

S
ABDE•CH=
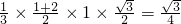
.…(8分)
(3)以H为原点建立如图所示的空间直角坐标系
则C(

),E(0,-

,1),F(
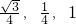
),∴

,

设平面CEF的法向量为

,由
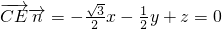
,

,得
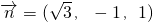
平面ABC的法向量为
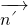
=(0,0,1)
∴cos
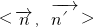
=
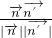
=

∴平面角ECD和平面ACB所成的锐二面角的余弦值

.
分析:(1)取BC中点G,连FG,AG.根据AE⊥面ABC,BD∥AE,可得BD⊥面ABC,从而BD⊥AG.进而可证AG⊥平面BCD.又可证四边形AEFG是平行四边形,所以EF∥AG,故EF⊥面BCD.
(2)设AB中点为H,则根据AE⊥面ABC,可得平面ABDE⊥平面ABC.所以CH⊥平面ABDE,即CH为四棱锥C-ABDE的高.从而可求四棱锥C-ABDE的体积.
(3)利用坐标表示点与向量,确定设平面CEF的法向量,平面ABC的法向量,利用向量的夹角公式,即可求得结论.
点评:本题以多面体为载体,考查线面垂直,考查几何体的体积,考查面面角,关键是利用向量的方法解决面面角,是一道综合题.

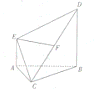 如图,在多面体ABCDE中,AE⊥面ABC,DB∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点.
如图,在多面体ABCDE中,AE⊥面ABC,DB∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点. 解:(1)取BC中点G点,连接AG,FG,如图1
解:(1)取BC中点G点,连接AG,FG,如图1 ,如图2
,如图2 SABDE•CH=
SABDE•CH=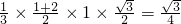 .…(8分)
.…(8分) ),E(0,-
),E(0,- ,1),F(
,1),F(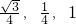 ),∴
),∴ ,
,
 ,由
,由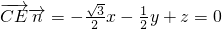 ,
, ,得
,得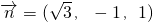
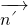 =(0,0,1)
=(0,0,1)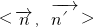 =
=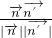 =
=
 .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1= (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=