
【题目】已知函数f(x)=Asin(ωx+φ),(x∈R,A>0,ω>0,|φ|< ![]() )的部分图象如图所示:
)的部分图象如图所示: 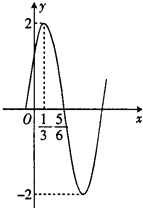
(1)试确定f(x)的解析式;
(2)若f( ![]() )=
)= ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:由图可知,A=2, ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,又ω>0,
,又ω>0,
∴T= ![]() =2,
=2,
∴ω=π;
由图可知,f(x)=Asin(ωx+φ)经过( ![]() ,2),
,2),
∴ ![]() ω+φ=
ω+φ= ![]() ,即
,即 ![]() +φ=
+φ= ![]() ,
,
∴φ= ![]() ,
,
∴f(x)=2sin(πx+ ![]() );
);
(2)解:∵f( ![]() )=
)= ![]() ,
,
∴2sin( ![]() +
+ ![]() )=
)= ![]() ,
,
∴sin( ![]() +
+ ![]() )=cos[
)=cos[ ![]() ﹣(
﹣( ![]() +
+ ![]() )]=cos(
)]=cos( ![]() ﹣
﹣ ![]() )=
)= ![]() ,
,
∴cos( ![]() ﹣α)=2
﹣α)=2 ![]() ﹣1=2×
﹣1=2× ![]() ﹣1=﹣
﹣1=﹣ ![]() .
.
【解析】(1)由图可知,A=2, ![]() =
= ![]() ,可求得ω,再利用
,可求得ω,再利用 ![]() ω+φ=
ω+φ= ![]() 可求得φ,从而可求得f(x)的解析式;(2)由(1)知f(x)的解析式,结合已知f(
可求得φ,从而可求得f(x)的解析式;(2)由(1)知f(x)的解析式,结合已知f( ![]() )=
)= ![]() ,可求得α的三角函数知,最后利用两角差的余弦计算即可求cos(
,可求得α的三角函数知,最后利用两角差的余弦计算即可求cos( ![]() ﹣α)的值.
﹣α)的值.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),在同一周期内,当x= ![]() 时,f(x)取得最大值3,当x=﹣
时,f(x)取得最大值3,当x=﹣ ![]() 时,f(x)取得最小值﹣3. (Ⅰ)求函数f(x)的解析式;
时,f(x)取得最小值﹣3. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程 ![]() =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 、
、 ![]() 为平面向量,若存在不全为零的实数λ,μ使得λ
为平面向量,若存在不全为零的实数λ,μ使得λ ![]() +μ
+μ ![]() =0,则称
=0,则称 ![]() 、
、 ![]() 线性相关,下面的命题中,
线性相关,下面的命题中, ![]() 、
、 ![]() 、
、 ![]() 均为已知平面M上的向量. ①若
均为已知平面M上的向量. ①若 ![]() =2
=2 ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
②若 ![]() 、
、 ![]() 为非零向量,且
为非零向量,且 ![]() ⊥
⊥ ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
③若 ![]() 、
、 ![]() 线性相关,
线性相关, ![]() 、
、 ![]() 线性相关,则
线性相关,则 ![]() 、
、 ![]() 线性相关;
线性相关;
④向量 ![]() 、
、 ![]() 线性相关的充要条件是
线性相关的充要条件是 ![]() 、
、 ![]() 共线.
共线.
上述命题中正确的是(写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinωxcosωx+2 ![]() sin2ωx﹣
sin2ωx﹣ ![]() (ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点, 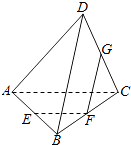
(1)求证:BD∥平面EFG;
(2)若AD=CD,AB=CB,求证:AC⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法点拨:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.(参考下表)
p(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.789 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com