
ЁОЬтФПЁПШчЭМЫљЪОЕФЁА8ЁБзжаЮЧњЯпЪЧгЩСНИіЙигкxжсЖдГЦЕФАыдВКЭвЛИіЫЋЧњЯпЕФвЛВПЗжзщГЩЕФЭМаЮЃЌЦфжаЩЯАыИідВЫљдкдВЗНГЬЪЧx2+y2Љ4yЉ4ЃН0ЃЌЫЋЧњЯпЕФзѓЁЂгвЖЅЕуAЁЂBЪЧИУдВгыxжсЕФНЛЕуЃЌЫЋЧњЯпгыАыдВЯрНЛгкгыxжсЦНааЕФжБОЖЕФСНЖЫЕуЃЎ
ЃЈ1ЃЉЪдЧѓЫЋЧњЯпЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉМЧЫЋЧњЯпЕФзѓЁЂгвНЙЕуЮЊF1ЁЂF2ЃЌЪддкЁА8ЁБзжаЮЧњЯпЩЯЧѓЕуPЃЌЪЙЕУЁЯF1PF2ЪЧжБНЧЃЎ
ЃЈ3ЃЉЙ§ЕуAзїжБЯпlЗжБ№НЛЁА8ЁБзжаЮЧњЯпжаЩЯЁЂЯТСНИіАыдВгкЕуMЁЂNЃЌЧѓ|MN|ЕФзюДѓГЄЖШЃЎ
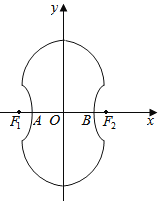
ЁОД№АИЁПЃЈ1ЃЉ![]() 1ЃЛЃЈ2ЃЉЃЈ
1ЃЛЃЈ2ЃЉЃЈ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЉЃЈ3ЃЉзюДѓГЄЖШЮЊ8
ЃЉЃЈ3ЃЉзюДѓГЄЖШЮЊ8
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіАыдВЕФдВаФКЭАыОЖЃЌЧѓЕУдВгыxжсЕФНЛЕуЃЌМДгаaЃН2ЃЌСюyЃН2ЃЌНтЕУНЛЕуЃЌДњШыЫЋЧњЯпЗНГЬЃЌНтЕУbЃЌНјЖјЕУЕНЫЋЧњЯпЕФЗНГЬЃЛ
ЃЈ2ЃЉЧѓГіНЙЕузјБъЃЌЁЯF1PF2ЪЧжБНЧЃЌдђЩшPЃЈxЃЌyЃЉЃЌдђгЩx2+y2ЃН8ЃЌСЊСЂСНАыдВЕФЗНГЬМАЫЋЧњЯпЗНГЬЃЌНтЕУНЛЕуЃЌзЂвтМьбщЃЌМДПЩЕУЕНЫљЧѓЕФPЕФзјБъЃЎ
ЃЈ3ЃЉЬжТлаБТЪЪЧЗёДцдкЃЌЧѓГі|MN|ЃЌМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЩЯАыИідВЫљдкдВЗНГЬЪЧx2+y2Љ4yЉ4ЃН0ЃЌдђдВаФЮЊЃЈ0ЃЌ2ЃЉЃЌАыОЖЮЊ2![]() ЃЎ
ЃЎ
дђЯТАыИідВЫљдкдВЕФдВаФЮЊЃЈ0ЃЌЉ2ЃЉЃЌАыОЖЮЊ2![]() ЃЎ
ЃЎ
ЫЋЧњЯпЕФзѓЁЂгвЖЅЕуAЁЂBЪЧИУдВгыxжсЕФНЛЕуЃЌМДЮЊЃЈЉ2ЃЌ0ЃЉЃЌЃЈ2ЃЌ0ЃЉЃЌМДaЃН2ЃЌ
гЩгкЫЋЧњЯпгыАыдВЯрНЛгкгыxжсЦНааЕФжБОЖЕФСНЖЫЕуЃЌдђСюyЃН2ЃЌНтЕУЃЌxЃНЁР2![]() ЃЎ
ЃЎ
МДгаНЛЕуЮЊЃЈЁР2![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
ЩшЫЋЧњЯпЕФЗНГЬЮЊ![]() 1ЃЈaЃО0ЃЌbЃО0ЃЉЃЌ
1ЃЈaЃО0ЃЌbЃО0ЃЉЃЌ
дђ![]() 1ЃЌЧвaЃН2ЃЌНтЕУЃЌbЃН2ЃЎ
1ЃЌЧвaЃН2ЃЌНтЕУЃЌbЃН2ЃЎ
дђЫЋЧњЯпЕФЗНГЬЮЊ![]() 1ЃЛ
1ЃЛ
ЃЈ2ЃЉЫЋЧњЯпЕФзѓЁЂгвНЙЕуЮЊF1ЃЈЉ2![]() ЃЌ0ЃЉЃЌF2ЃЈ2
ЃЌ0ЃЉЃЌF2ЃЈ2![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ШєЁЯF1PF2ЪЧжБНЧЃЌдђЩшPЃЈxЃЌyЃЉЃЌдђгаx2+y2ЃН8ЃЌ
гЩ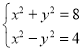 НтЕУЃЌx2ЃН6ЃЌy2ЃН2ЃЎЙЪPЕФзјБъЮЊЃЈ
НтЕУЃЌx2ЃН6ЃЌy2ЃН2ЃЎЙЪPЕФзјБъЮЊЃЈ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
гЩ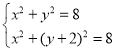 НтЕУЃЌyЃН-1ЃЌВЛТњзуЬтвтЃЌЩсШЅЃЎ
НтЕУЃЌyЃН-1ЃЌВЛТњзуЬтвтЃЌЩсШЅЃЎ
гЩ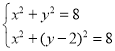 НтЕУЃЌyЃН1ЃЌВЛТњзуЬтвтЃЌЩсШЅЃЎ
НтЕУЃЌyЃН1ЃЌВЛТњзуЬтвтЃЌЩсШЅЃЎ
ЙЪдкЁА8ЁБзжаЮЧњЯпЩЯЫљЧѓЕуPЕФзјБъЮЊЃЈ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉЩшMЃЌNЕФКсзјБъЗжБ№ЮЊxMЃЌxNЃЎ
ЂйжБЯпlЕФаБТЪВЛДцдкЪБЃЌ|MN|ЃН8ЃЛ
ЂкжБЯпlЕФаБТЪДцдкЪБЃЌЩшЗНГЬЮЊyЃНkЃЈx+2ЃЉЃЈ![]() Лђ
Лђ![]() ЃЉЃЌ
ЃЉЃЌ
ДњШыx2+y2Љ4yЉ4ЃН0ЃЌПЩЕУЃЈk2+1ЃЉx2+ЃЈ4k2Љ4kЃЉx+4k2Љ8kЉ4ЃН0ЃЌ
ЁрЉ2xM![]() ЃЌ
ЃЌ
ЁрxM![]() ЃЌ
ЃЌ
ЭЌРэxN![]() ЃЌ
ЃЌ
Ёр|MN|![]() |xMЉxN|
|xMЉxN|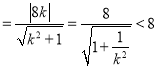 ЃЌ
ЃЌ
злЩЯЃК|MN|ЕФзюДѓГЄЖШЮЊ8ЃЎ


 ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШ§Ртжљ![]() жаЃЌВрРтгыЕзУцДЙжБЃЌ
жаЃЌВрРтгыЕзУцДЙжБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛжЛвЉгУРЅГцЕФВњТбЪ§yгывЛЖЈЗЖЮЇФкЕФЮТЖШxгаЙиЃЌЯжЪеМЏСЫИУжжвЉгУРЅГцЕФ6зщЙлВтЪ§ОнШчЯТБэЃК
ЮТЖШx/Ёц | 21 | 23 | 24 | 27 | 29 | 32 |
ВњТбЪ§y/Иі | 6 | 11 | 20 | 27 | 57 | 77 |
ОМЦЫуЕУЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЯпадЛиЙщФЃаЭЕФВаВюЦНЗНКЭ
ЯпадЛиЙщФЃаЭЕФВаВюЦНЗНКЭ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Цфжа![]() ЗжБ№ЮЊЙлВтЪ§ОнжаЕФЮТЖШКЭВњТбЪ§ЃЌ
ЗжБ№ЮЊЙлВтЪ§ОнжаЕФЮТЖШКЭВњТбЪ§ЃЌ![]()
ЃЈ1ЃЉШєгУЯпадЛиЙщФЃаЭЃЌЧѓyЙигкxЕФЛиЙщЗНГЬ![]() ЃЈОЋШЗЕН0.1ЃЉЃЛ
ЃЈОЋШЗЕН0.1ЃЉЃЛ
ЃЈ2ЃЉШєгУЗЧЯпадЛиЙщФЃаЭЧѓЕУyЙигкxЕФЛиЙщЗНГЬЮЊ![]() ЃЌЧвЯрЙижИЪ§
ЃЌЧвЯрЙижИЪ§![]() .
.
ЂйЪдгы1жаЕФЛиЙщФЃаЭЯрБШЃЌгУ![]() ЫЕУїФФжжФЃаЭЕФФтКЯаЇЙћИќКУ.
ЫЕУїФФжжФЃаЭЕФФтКЯаЇЙћИќКУ.
ЂкгУФтКЯаЇЙћКУЕФФЃаЭдЄВтЮТЖШЮЊ35ЁцЪБИУгУФФжжвЉгУРЅГцЕФВњТбЪ§ЃЈНсЙћШЁећЪ§ЃЉ
ИНЃКвЛзщЪ§Он![]() ЦфЛиЙщжБЯп
ЦфЛиЙщжБЯп![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЮЊ
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЮЊ ЃЌ
ЃЌ![]() ЃЛЯрЙижИЪ§
ЃЛЯрЙижИЪ§ .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЛЭЈжИЪ§ЪЧжИНЛЭЈгЕЖТжИЪ§ЕФМђГЦЃЌЪЧзлКЯЗДгГЕРТЗЭјГЉЭЈЛђгЕЖТЕФИХФюаджИЪ§жЕЃЌМЧНЛЭЈжИЪ§ЮЊ![]() ЃЌЦфЗЖЮЇЮЊ
ЃЌЦфЗЖЮЇЮЊ![]() ЃЌЗжБ№гаЮхИіМЖБ№ЃК
ЃЌЗжБ№гаЮхИіМЖБ№ЃК![]() ЃЌГЉЭЈЃЛ
ЃЌГЉЭЈЃЛ![]() ЃЌЛљБОГЉЭЈЃЛ
ЃЌЛљБОГЉЭЈЃЛ![]() ЃЌЧсЖШгЕЖТЃЛ
ЃЌЧсЖШгЕЖТЃЛ![]() ЃЌжаЖШгЕЖТЃЛ
ЃЌжаЖШгЕЖТЃЛ![]() ЃЌбЯжигЕЖТ.дкЭэИпЗхЪБЖЮЃЈ
ЃЌбЯжигЕЖТ.дкЭэИпЗхЪБЖЮЃЈ![]() ЃЉЃЌДгФГЪаНЛЭЈжИЛгжааФбЁШЁСЫЪаЧј20ИіНЛЭЈТЗЖЮЃЌвРОнЦфНЛЭЈжИЪ§Ъ§ОнЛцжЦЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.
ЃЉЃЌДгФГЪаНЛЭЈжИЛгжааФбЁШЁСЫЪаЧј20ИіНЛЭЈТЗЖЮЃЌвРОнЦфНЛЭЈжИЪ§Ъ§ОнЛцжЦЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.
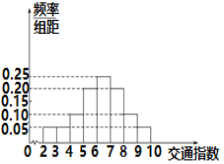
(1)ЧѓГіЧсЖШгЕЖТЁЂжаЖШгЕЖТЁЂбЯжигЕЖТЕФТЗЖЮЕФИіЪ§ЃЛ
(2)гУЗжВуГщбљЕФЗНЗЈДгЧсЖШгЕЖТЁЂжаЖШгЕЖТЁЂбЯжигЕЖТЕФТЗЖЮжаЙВГщШЁ6ИіТЗЖЮЃЌЧѓвРДЮГщШЁЕФШ§ИіМЖБ№ТЗЖЮЕФИіЪ§ЃЛ
(3)Дг(2)жаГщШЁЕФ6ИіТЗЖЮжаШЮШЁ2ИіЃЌЧѓжСЩйга1ИіТЗЖЮЮЊЧсЖШгЕЖТЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
![]() ЕФвЛЖЮЭМЯёШчЭМЫљЪО.
ЕФвЛЖЮЭМЯёШчЭМЫљЪО.

ЃЈ1ЃЉЧѓДЫКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓДЫКЏЪ§дк![]() ЩЯЕФЕЅЕїЕндіЧјМф.
ЩЯЕФЕЅЕїЕндіЧјМф.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕЮЊШЗЖЈЯТвЛФъЭЖШыФГжжВњЦЗЕФбаЗЂЗбгУЃЌашСЫНтФъбаЗЂЗбгУ![]() ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉЖдФъЯњЪлСП
ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉЖдФъЯњЪлСП![]() ЃЈЕЅЮЛЃКЧЇЭђМўЃЉЕФгАЯьЃЌЭГМЦСЫНќ
ЃЈЕЅЮЛЃКЧЇЭђМўЃЉЕФгАЯьЃЌЭГМЦСЫНќ![]() ФъЭЖШыЕФФъбаЗЂЗбгУ
ФъЭЖШыЕФФъбаЗЂЗбгУ![]() гыФъЯњЪлСП
гыФъЯњЪлСП![]() ЕФЪ§ОнЃЌЕУЕНЩЂЕуЭМШчЭМЫљЪОЃЎ
ЕФЪ§ОнЃЌЕУЕНЩЂЕуЭМШчЭМЫљЪОЃЎ
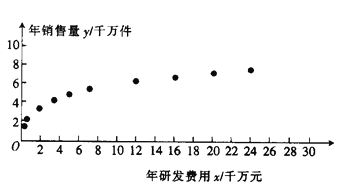
(1)РћгУЩЂЕуЭМХаЖЯ![]() КЭ
КЭ![]() ЃЈЦфжа
ЃЈЦфжа![]() ОљЮЊДѓгк
ОљЮЊДѓгк![]() ЕФГЃЪ§ЃЉФФвЛИіИќЪЪКЯзїЮЊФъЯњЪлСП
ЕФГЃЪ§ЃЉФФвЛИіИќЪЪКЯзїЮЊФъЯњЪлСП![]() КЭФъбаЗЂЗбгУ
КЭФъбаЗЂЗбгУ![]() ЕФЛиЙщЗНГЬРраЭЃЈжЛвЊИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉ
ЕФЛиЙщЗНГЬРраЭЃЈжЛвЊИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉ
(2)ЖдЪ§ОнзїГіШчЯТДІРэЃЌСю![]() ЃЌЕУЕНЯрЙиЭГМЦСПЕФжЕШчЯТБэЃКИљОнЕк(1)ЮЪЕФХаЖЯНсЙћМАБэжаЪ§ОнЃЌЧѓ
ЃЌЕУЕНЯрЙиЭГМЦСПЕФжЕШчЯТБэЃКИљОнЕк(1)ЮЪЕФХаЖЯНсЙћМАБэжаЪ§ОнЃЌЧѓ![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬЃЛ
ЕФЛиЙщЗНГЬЃЛ
|
|
|
|
15 | 15 | 28.25 | 56.5 |
(3)вбжЊЦѓвЕФъРћШѓ![]() ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉгы
ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉгыЕФЙиЯЕЮЊ
![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЃЌИљОнЕк(2)ЮЪЕФНсЙћХаЖЯЃЌвЊЪЙЕУИУЦѓвЕЯТвЛФъЕФФъРћШѓзюДѓЃЌдЄМЦЯТвЛФъгІЭЖШыЖрЩйбаЗЂЗбгУ?
ЃЉЃЌИљОнЕк(2)ЮЪЕФНсЙћХаЖЯЃЌвЊЪЙЕУИУЦѓвЕЯТвЛФъЕФФъРћШѓзюДѓЃЌдЄМЦЯТвЛФъгІЭЖШыЖрЩйбаЗЂЗбгУ?
ИНЃКЖдгквЛзщЪ§Он![]() ЃЌЦфЛиЙщжБЯп
ЃЌЦфЛиЙщжБЯп![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ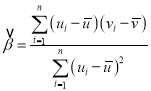 ЃЌ
ЃЌ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж12ЗжЃЉ
ШчЭМдкжБШ§РтжљABCЁЊA1B1C1жаЃЌAC=3ЃЌBC=4ЃЌAB=5ЃЌAA1=4,ЕуDЪЧABЕФ
жаЕу.
(1) ЧѓжЄЃК ACЁЭBC1
(2) ЧѓжЄЃКAC1ЁЮЦНУцCDB1
(3) ЧѓвьУцжБЯпAC1гыB1CЫљГЩНЧЕФгрЯвжЕ.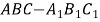
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЮЊЭждВ
ЗжБ№ЮЊЭждВ![]() ЕФзѓЁЂгвНЙЕу.ЩшВЛОЙ§НЙЕу
ЕФзѓЁЂгвНЙЕу.ЩшВЛОЙ§НЙЕу![]() ЕФжБЯп
ЕФжБЯп![]() гыЭждВНЛгкСНИіВЛЭЌЕФЕу
гыЭждВНЛгкСНИіВЛЭЌЕФЕу![]() ЁЂ
ЁЂ![]() ЃЌНЙЕу
ЃЌНЙЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() .ШєжБЯп
.ШєжБЯп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФаБТЪвРДЮГЩЕШВюЪ§СаЃЌЧѓ
ЕФаБТЪвРДЮГЩЕШВюЪ§СаЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жа,
жа,![]() ОЙ§дЕуЕФжБЯп
ОЙ§дЕуЕФжБЯп![]() НЋ
НЋ![]() ЗжГЩзѓЁЂгвСНВПЗж,МЧзѓЁЂгвСНВПЗжЕФУцЛ§ЗжБ№ЮЊ
ЗжГЩзѓЁЂгвСНВПЗж,МЧзѓЁЂгвСНВПЗжЕФУцЛ§ЗжБ№ЮЊ![]() ,дђ
,дђ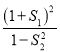 ШЁЕУзюаЁжЕЪБ,жБЯп
ШЁЕУзюаЁжЕЪБ,жБЯп![]() ЕФаБТЪЃЈ ЃЉ
ЕФаБТЪЃЈ ЃЉ
A.ЕШгк1B.ЕШгк![]() C.ЕШгк
C.ЕШгк![]() D.ВЛДцдк
D.ВЛДцдк
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com