
函数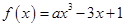 对于
对于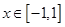 总有
总有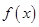 ≥0 成立,则
≥0 成立,则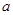 的取值集合为 .
的取值集合为 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| an |
| 1 |
| (p-1)•3qx+1 |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源:南汇区二模 题型:解答题
| 1 |
| an |
| 1 |
| (p-1)•3qx+1 |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源: 题型:
①对于任意x∈[0,1],总有f(x)≥3,且f(1)=4;
②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.
(1)求f(0)的值;
(2)求证:f(x)≤4;
(3)当x∈(![]() ](n=1,2,3,…)时,试证明f(x)<3x+3.
](n=1,2,3,…)时,试证明f(x)<3x+3.
(文)如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1)、(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.

(1)求证:y1y2=-p2;
(2)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;
(3)若![]() =0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
=0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年山东省济宁一中高三(上)第一次反馈练习数学试卷(文科)(解析版) 题型:解答题
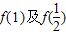 的值(写成关于p的表达式);
的值(写成关于p的表达式);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com