
【题目】已知:函数f(x)= ![]() (a>0且a≠1).
(a>0且a≠1).
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)设a=![]() ,解不等式f(x)>0.
,解不等式f(x)>0.
【答案】(1) (-1,1);(2)见解析;(3) {x|-1<x<0}
【解析】试题分析:(I)根据对数函数有意义可知真数要大于0,列不等式组,解之即可求出函数的定义域;(Ⅱ)根据函数的奇偶性的定义进行判定,计箄![]() 与
与![]() 的关系,从而确定函数的奇偶性;(Ⅲ)将
的关系,从而确定函数的奇偶性;(Ⅲ)将![]() 代入,根据函数的定义域和函数的单调性列不等式组,解之即可求出
代入,根据函数的定义域和函数的单调性列不等式组,解之即可求出![]() 的范围.
的范围.
试题解析:(Ⅰ)由题知: ![]() ,解得:-1<x<1,所以函数f(x)的定义域为(-1,1);
,解得:-1<x<1,所以函数f(x)的定义域为(-1,1);
(Ⅱ)奇函数,
证明:因为函数f(x)的定义域为(-1,1),所以对任意x∈(-1,1),
f(-x)= ![]() =
=![]() =-f(x)
=-f(x)
所以函数f(x)是奇函数;
(Ⅲ)由题知: ![]() 即有
即有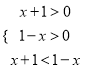 ,解得:-1<x<0,
,解得:-1<x<0,
所以不等式f(x)>0的解集为{x|-1<x<0}.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】某厂生产一种产品的固定成本(即固定投入)为0.5万元,但每生产一百件这样的产品,需要增加可变成本(即另增加投入)0.25万元. 市场对此产品的年需求量为500件,销售的收入函数为![]() =
=![]() (单位:万元),其中
(单位:万元),其中![]() 是产品售出的数量(单位:百件).
是产品售出的数量(单位:百件).
(1)该公司这种产品的年产量为![]() 百件,生产并销售这种产品所得到的利润为当年产量
百件,生产并销售这种产品所得到的利润为当年产量![]() 的函数
的函数![]() ,求
,求![]() ;
;
(2)当年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校,在课堂上,李老师请学生画出自行车行进路程s(千米)与行进时间x(秒)的函数图象的示意图,你认为正确的是
A. 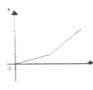 B.
B. 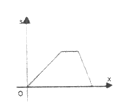
C. 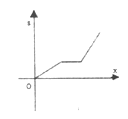 D.
D. 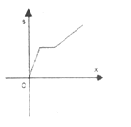
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是A1B1的中点. 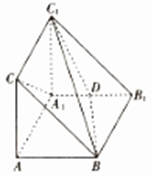
(1)求证:A1C∥平面BDC1;
(2)若AB⊥AC,且AB=AC= ![]() AA1 , 求二面角A﹣BD﹣C1的余弦值.
AA1 , 求二面角A﹣BD﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为F(c,0)的椭圆M: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

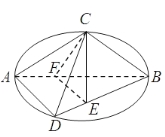
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
A.x∈R,f(x)≤f(x0)
B.x∈R,f(x)≥f(x0)
C.x∈R,f(x)≤f(x0)
D.x∈R,f(x)≥f(x0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com