
【题目】已知直线l经过点(1,﹣2),且与直线m:4x﹣3y+1=0平行;
(1)求直线l的方程;
(2)求直线l被圆x2+y2=9所截得的弦长.
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】为了解高三年级学生寒假期间的学习情况,某学校抽取了甲、乙两班作为对象,调查这两个班的学生在寒假期间平均每天学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生平均每天学习时间在区间![]() 的有8人.
的有8人.
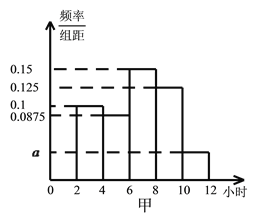

(I)求直方图中![]() 的值及甲班学生平均每天学习时间在区间
的值及甲班学生平均每天学习时间在区间![]() 的人数;
的人数;
(II)从甲、乙两个班平均每天学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() =(2sinx,2cosx),
=(2sinx,2cosx), ![]() =(cosx,﹣cosx),f(x)=
=(cosx,﹣cosx),f(x)= ![]() .
.
(1)若 ![]() 与
与 ![]() 共线,且x∈(
共线,且x∈( ![]() ,π),求x的值;
,π),求x的值;
(2)求函数f(x)的周期;
(3)若对任意x∈[0, ![]() ]不等式m﹣2≤f(x)≤m+
]不等式m﹣2≤f(x)≤m+ ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程 ![]() =﹣1表示的曲线即为函数y=f(x),有如下结论:( ) ①函数f(x)在R上单调递减;
=﹣1表示的曲线即为函数y=f(x),有如下结论:( ) ①函数f(x)在R上单调递减;
②函数F(x)=4f(x)+3x不存在零点;
③函数y=f(x)的值域是R;
④若函数g(x)和f(x)的图象关于原点对称,则函数y=g(x)的图象就是方程 ![]() =﹣1确定的曲线.
=﹣1确定的曲线.
其中所有正确的命题序号是( )
A.①②
B.②③
C.①③④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2 , 人行道的宽度分别为4m和10m.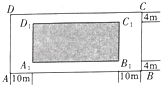
(1)若休闲区的长A1B1=x m,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
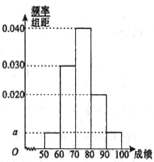
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin ωxcos ωx-sin2ωx+1(ω>0)图象的相邻两条对称轴之间的距离为
sin ωxcos ωx-sin2ωx+1(ω>0)图象的相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求ω的值及函数f(x)的单调递减区间;
(Ⅱ)如图,在锐角三角形ABC中有f(B)=1,若在线段BC上存在一点D使得AD=2,且AC=![]() ,CD=
,CD=![]() -1,求三角形ABC的面积.
-1,求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)设全集为R,A={x|3<x<7},B={x|4<x<10},求R(A∪B)及(RA)∩B.
(2)C={x|a﹣4≤x≤a+4},且A∩C=A,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com