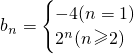Question

已知数列{a_n}的前n项和S_n=2n²+n-1，数列{b_n}满足b₁+3b₂+…+（2n-1）b_n=（2n-3）•2ⁿ⁺¹，
求：数列{a_nb_n}的前n项和T_n．

Answer 1

解：当n≥2时，a_n=S_n-S_n-1=4n-1，而a₁=2，
∴
当n≥2时，（2n-1）•b_n=（2n-3）•2ⁿ⁺¹-（2n-5）•2ⁿ=2ⁿ（2n-1）
∴b_n=2ⁿ，而b₁=-4，∴
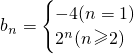
∴T_n=-8+[2²×7+2³×11+…+2ⁿ（4n-1）]
记S=2²×7+2³×11+2⁴×15+…+2ⁿ（4n-1）①
∴2S=2³×7+2⁴×11+2⁵×15++2ⁿ（4n-5）+2ⁿ⁺¹（4n-1）②
①-②得：
∴-S=28+4（2³+2⁴++2ⁿ）-2ⁿ⁺¹（4n-1）
-S=28+32（2^n-1-1）-2ⁿ⁺¹（4n-1）=-4+2ⁿ⁺¹（5-4n）
∴S=4+2ⁿ⁺¹（4n-5）
T_n=2ⁿ⁺¹（4n-5）-4
分析：利用递推公式a_n=s_n-s_n-1（n≥2），a₁=s₁求数列a_n的通项公式，利用同样的方法求出数列b_n的通项，从而可得数列a_n，b_n分别是从第二项开始的等差（等比）数列，则对数列a_n•b_n求和应用乘“公比”错位相减
点评：本题主要考查了利用递推公式由“和”求“项”，体现了转化思想，由等比数列与等差数列的积构成的数列的求和，用乘“公比”错位相减，其中的公比是指成等比数列的公比．