
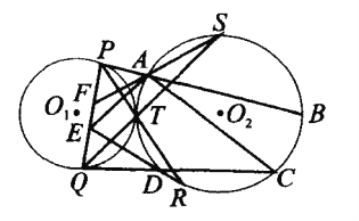
【题目】如图,两圆外切于点T, PQ为![]() 的弦,直线PT、QT分别交
的弦,直线PT、QT分别交![]() 于点R、S,分别过P、Q作
于点R、S,分别过P、Q作![]() 的切线依次交
的切线依次交![]() 于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:
于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:![]() 。
。
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为![]() :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4纸的长度为( )
,那么A4纸的长度为( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过点P作圆
,点P在直线l上,过点P作圆![]() 的切线PA,PB,切点为A,B.
的切线PA,PB,切点为A,B.
(1)若![]() ,求点P的坐标;
,求点P的坐标;
(2)求证:经过A,P,![]() 三点的圆必经过异于
三点的圆必经过异于![]() 的某个定点,并求该定点的坐标.
的某个定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
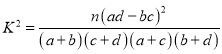 (其中
(其中 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合S={1,2,3,4,5,6},一一映射f:S→S满足条件:对于任意的x∈S,有f(f(f(x)))=x。则满足条件的映射f的个数是( )。
A. 81 B. 80 C. 40 D. 27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P—A1B1C1D1,下部的形状是正四棱柱ABCD—A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
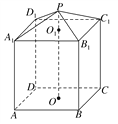
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.
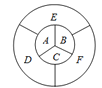
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com