
分析 (I)利用f(x)=xc(x)-3000,即可得出结论;
(II)分段讨论,0<x≤50时,f(x)=xc(x)-3000=-3x2+192x-2980,x=32时,f(x)max=f(32)=92;x>50时,f(x)=xc(x)-3000=-$\frac{7200}{x}$-2x+640=640-(2x+$\frac{7200}{x}$),利用基本不等式,可得结论.
解答 解:(I)0<x≤50时,f(x)=xc(x)-3000=-3x2+192x-2980,
x>50时,f(x)=xc(x)-3000=-$\frac{7200}{x}$-2x+640,
∴f(x)=$\left\{\begin{array}{l}{-3{x}^{2}+192x-2980,0<x≤50}\\{-\frac{7200}{x}-2x+640,x>50}\end{array}\right.$;
(II)0<x≤50时,f(x)=xc(x)-3000=-3x2+192x-2980,x=32时,f(x)max=f(32)=92;
x>50时,f(x)=xc(x)-3000=-$\frac{7200}{x}$-2x+640=640-(2x+$\frac{7200}{x}$)≤400,
当且仅当2x=$\frac{7200}{x}$,即x=60时,f(x)max=f(60)=400,
∵400>92,
∴该单位年处理工厂废气量为60万升时,所获得的利润最大,最大利润为400万元.
点评 本题考查了分段函数模型的应用题目,并且考查了求二次函数的最值,利用基本不等式求函数的最值等问题,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
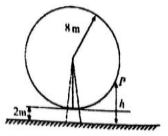 如图,一个摩天轮的半径为8m,每12min旋转一周,最低点离地面为2m,若摩天轮边缘某点P从最低点按逆时针方向开始旋转,则点P离地面的距离h(m)与时间t(min)之间的函数关系是( )
如图,一个摩天轮的半径为8m,每12min旋转一周,最低点离地面为2m,若摩天轮边缘某点P从最低点按逆时针方向开始旋转,则点P离地面的距离h(m)与时间t(min)之间的函数关系是( )| A. | h=8cost+10 | B. | h=-8cos$\frac{π}{3}$t+10 | C. | h=-8sin$\frac{π}{6}$t+10 | D. | h=-8cos$\frac{π}{6}$t+10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(-\frac{1}{2},0)$和$(\frac{1}{2},+∞)$ | C. | $(\frac{1}{2},+∞)$ | D. | $(-∞,-\frac{1}{2})$和$(0,\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 愿意参加 | 不愿意参加 | 合计 | |
| 城填生 | 50 | 25 | 75 |
| 农村生 | 10 | 15 | 25 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a≥2 | C. | a≥3 | D. | a≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,为测量塔高AB,选取与塔底B在同一水平面内的两点C、D,在C、D两点处测得塔顶A的仰角分别为45°,30°,又测得∠CBD=30°,CD=50米,则塔高AB=( )
如图,为测量塔高AB,选取与塔底B在同一水平面内的两点C、D,在C、D两点处测得塔顶A的仰角分别为45°,30°,又测得∠CBD=30°,CD=50米,则塔高AB=( )| A. | 50米 | B. | 25$\sqrt{3}$米 | C. | 25米 | D. | 50$\sqrt{3}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com