
 的图象过点(4,-1)
的图象过点(4,-1)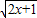 在∈[-
在∈[- ,+∞)上减函数,f(0)•f(4)<0,从而可判断f(x)在其定义域上有且只有一个零点;
,+∞)上减函数,f(0)•f(4)<0,从而可判断f(x)在其定义域上有且只有一个零点;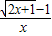 =
=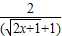 恒成立即可.
恒成立即可.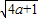 =-1,解之得a=2…2
=-1,解之得a=2…2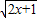 ,定义域为x∈[-
,定义域为x∈[- ,+∞)…3
,+∞)…3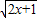 在∈[-
在∈[- ,+∞)上是增函数,
,+∞)上是增函数,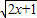 在∈[-
在∈[- ,+∞)上减函数,…5
,+∞)上减函数,…5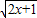 +mx>1即mx>
+mx>1即mx>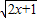 -1,
-1,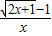 …9
…9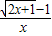 =
=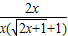 =
= ,
,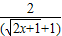 <1…11
<1…11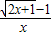 =
=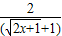 的转化与应用,属于难题.
的转化与应用,属于难题. 

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(05年福建卷文)(12分)
已知函数![]() 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高一上学期期末质量检测数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值;
(Ⅲ)若 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期第一次阶段考数学理科试卷 题型:解答题
已知函数 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
.
(1)求函数 的解析式; (2)求函数
的解析式; (2)求函数 的单调区间
的单调区间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com