
【题目】已知多面体![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
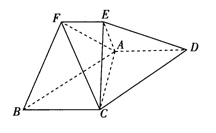
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 夹角的正弦值为
夹角的正弦值为![]() ,求
,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
,![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入-成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如表统计数据表:
收入x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据如表可得回归直线方程y= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户收入为20万元家庭年支出为( )
,据此估计,该社区一户收入为20万元家庭年支出为( )
A.11.4万元
B.11.8万元
C.15.2万元
D.15.6万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,﹣4),且倾斜角为 ![]() ,圆C的极坐标方程为ρ=4cosθ.
,圆C的极坐标方程为ρ=4cosθ.
(1)求直线l的参数方程和圆C的直角坐标方程;
(2)若直线l和圆C相交于A、B两点,求|PA||PB|及弦长|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x+a2x+3,a∈R
(1)当a=﹣4时,且x∈[0,2],求函数f(x)的值域;
(2)若f(x)>0在(0,+∞)对任意的实数x恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1.
,AB=2,PA=1. 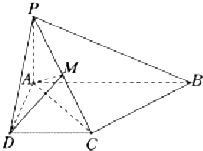
(1)求证:BC⊥平面PAC;
(2)若M是PC的中点,求二面角M﹣AD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)求曲线![]() 与
与![]() 交点的极坐标,其中
交点的极坐标,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[﹣1,2m]上不具有单调性,求实数m的取值范围;
(2)若f(1)=g(1).
(ⅰ)求实数a的值;
(ⅱ)设 ![]() ,t2=g(x),
,t2=g(x), ![]() ,当x∈(0,1)时,试比较t1 , t2 , t3的大小.
,当x∈(0,1)时,试比较t1 , t2 , t3的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com