
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)设函数![]() ,若对
,若对![]() ,
,![]() 恒不小于
恒不小于![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1) 极小值为![]() ,没有极大值 (2)
,没有极大值 (2) ![]()
【解析】
试题分析:(1)求导数![]() ,解f′(x)<0和f′(x)>0便可得出函数f(x)的单调区间,从而求出函数f(x)的极小值,并判断没有极大值;(2)根据条件可得出,对任意的x∈R,都有
,解f′(x)<0和f′(x)>0便可得出函数f(x)的单调区间,从而求出函数f(x)的极小值,并判断没有极大值;(2)根据条件可得出,对任意的x∈R,都有![]() 成立,然后令
成立,然后令![]() ,求导
,求导![]() ,讨论m的取值,根据导数符号求函数的最小值,从而得出m+n≤2m-mlnm,同样根据导数便可求出2m-mlnm的最大值,这样即可求出m+n的最大值
,讨论m的取值,根据导数符号求函数的最小值,从而得出m+n≤2m-mlnm,同样根据导数便可求出2m-mlnm的最大值,这样即可求出m+n的最大值
试题解析:(1)依题意![]() ,
,
令![]() 得
得![]()
令![]() 得
得![]()
故函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
故函数![]() 的极小值为
的极小值为![]() ,没有极大值。
,没有极大值。
(2)依题意对![]() ,即
,即![]() ,即
,即![]() 恒成立
恒成立
令![]() ,则
,则![]()
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,没有最小值,不符题意,舍去。
上单调递增,没有最小值,不符题意,舍去。
②若![]() ,令
,令![]() 得
得![]()
当![]() ,即
,即![]() 时,
时,![]() 单调递减;
单调递减;
当![]() ,即
,即![]() 时,
时,![]() 单调递增。
单调递增。
故![]()
故![]()
令![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
故![]() ,即
,即![]() ,即
,即![]() 的最大值是
的最大值是![]() 。
。


科目:高中数学 来源: 题型:
【题目】关于简单随机抽样的特点,有以下几种说法,其中不正确的是( )
A.要求总体中的个体数有限
B.从总体中逐个抽取
C.这是一种不放回抽样
D.每个个体被抽到的机会不一样,与先后顺序有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间![]() 上的函数
上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ,当
,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间
为区间![]() 上的“平底型”函数.
上的“平底型”函数.
(1)判断函数![]() 和
和![]() 是否为
是否为![]() 上的“平底型”函数?
上的“平底型”函数?
(2)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 是椭圆的两个顶点,
是椭圆的两个顶点,![]() ,
,![]() ,若点
,若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.直线
的一个“椭点”.直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,已知以
,已知以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试探讨![]() 的面积
的面积![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.
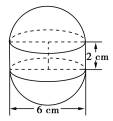
(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com