
【题目】科学家发现某种特别物质的温度![]() (单位:摄氏度)随时间
(单位:摄氏度)随时间![]() (时间:分钟)的变化规律满足关系式:
(时间:分钟)的变化规律满足关系式:![]() (
(![]() ,
,![]() ).
).
(1)若![]() ,求经过多少分钟,该物质的温度为5摄氏度;
,求经过多少分钟,该物质的温度为5摄氏度;
(2)如果该物质温度总不低于2摄氏度,求![]() 的取值范围.
的取值范围.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,数列
,数列![]() 满足条件:对于
满足条件:对于![]() ,
,![]() ,且
,且![]() ,并有关系式:
,并有关系式:![]() ,又设数列
,又设数列![]() 满足
满足![]() (
(![]() 且
且![]() ,
,![]() ).
).
(1)求证数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)试问数列![]() 是否为等差数列,如果是,请写出公差,如果不是,说明理由;
是否为等差数列,如果是,请写出公差,如果不是,说明理由;
(3)若![]() ,记
,记![]() ,
,![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,不等式
,不等式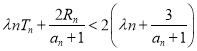 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中万事万物都是有关联的,所有直线中有关联直线,所有点中也有相关点,现在定义:平面内如果两点![]() 、
、![]() 都在函数
都在函数![]() 的图像上,而且满足
的图像上,而且满足![]() 、
、![]() 两点关于原点对称,则称点对(
两点关于原点对称,则称点对(![]() 、
、![]() )是函数
)是函数![]() 的“相关对称点对”(注明:点对(
的“相关对称点对”(注明:点对(![]() 、
、![]() )与(
)与(![]() 、
、![]() )看成同一个“相关对称点对”).已知函数
)看成同一个“相关对称点对”).已知函数 ,则这个函数的“相关对称点对”有( )
,则这个函数的“相关对称点对”有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上10,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.12.8 3.6 B.2.8 13.6 C.12.8 13.6 D.13.6 12.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,AC、BD交于点O,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
中,底面ABCD为矩形,AC、BD交于点O,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.

(1)求证:BD⊥平面PAC;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会为研究该校学生的性别与语文、数学、英语成绩这3个变量之间的关系,随机抽查了100名学生,得到某次期末考试的成绩数据如表1至表3,根据表中数据可知该校学生语文、数学、英语这三门学科中( )
表1 | 表2 | 表3 | |||||||||||||
语文 性别 | 不及格 | 及格 | 总计 | 数学 性别 | 不及格 | 及格 | 总计 | 英语 性别 | 不及格 | 及格 | 总计 | ||||
男 | 14 | 36 | 50 | 男 | 10 | 40 | 50 | 男 | 25 | 25 | 50 | ||||
女 | 16 | 34 | 50 | 女 | 20 | 30 | 50 | 女 | 5 | 45 | 50 | ||||
总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | ||||
A.语文成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
B.数学成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
C.英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
D.英语成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
查看答案和解析>>
科目:高中数学 来源: 题型:
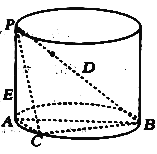
【题目】如图,![]() 是圆柱的直径,
是圆柱的直径,![]() 是圆柱的母线,
是圆柱的母线,![]() ,
,![]() ,点
,点![]() 是圆柱底面圆周上的点.
是圆柱底面圆周上的点.
(1)求三棱锥![]() 体积的最大值;
体积的最大值;
(2)若![]() ,
,![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的三等分点,点
的三等分点,点![]() 是线段
是线段![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com