
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .平面
.平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.
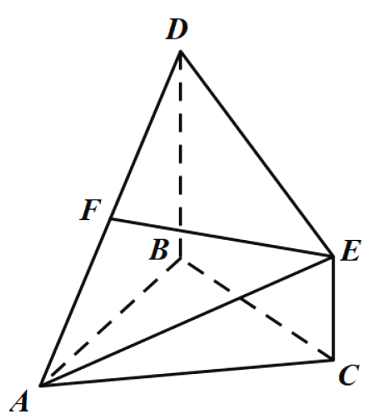
(1)求证:![]() 平面ABC;
平面ABC;
(2)求证:平面![]() 平面ABD.
平面ABD.
科目:高中数学 来源: 题型:
【题目】如图,![]() 点在正方体
点在正方体![]() 的棱
的棱![]() 上(不含端点),给出下列五个命题:
上(不含端点),给出下列五个命题:
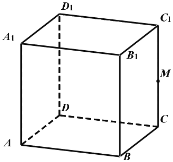
①过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]() ,
,![]() 都是异面直线;
都是异面直线;
②过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]() ,
,![]() 都相交;
都相交;
③过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]() ,
,![]() 都垂直;
都垂直;
④过![]() 点有无数个平面与直线
点有无数个平面与直线![]() ,
,![]() 都相交;
都相交;
⑤过![]() 点有无数个平面与直线
点有无数个平面与直线![]() ,
,![]() 都平行;
都平行;
其中真命题是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三学生为了迎接高考,要经常进行模拟考试,锻炼应试能力,某学生从升入高三到高考要参加![]() 次模拟考试,下面是高三第一学期某学生参加
次模拟考试,下面是高三第一学期某学生参加![]() 次模拟考试的数学成绩表:
次模拟考试的数学成绩表:
模拟考试第 |
|
|
|
|
|
考试成绩 |
|
|
|
|
|
(1)已知该考生的模拟考试成绩![]() 与模拟考试的次数
与模拟考试的次数![]() 满足回归直线方程
满足回归直线方程![]() ,若高考看作第
,若高考看作第![]() 次模拟考试,试估计该考生的高考数学成绩;
次模拟考试,试估计该考生的高考数学成绩;
(2)把![]() 次模拟考试的成绩单放在五个相同的信封中,从中随机抽取
次模拟考试的成绩单放在五个相同的信封中,从中随机抽取![]() 个信封研究成绩,求抽取的
个信封研究成绩,求抽取的![]() 个信封中恰有
个信封中恰有![]() 个成绩不等于平均值
个成绩不等于平均值![]() 的概率.
的概率.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:①任意两条直线都可以确定一个平面;②若两个平面有3个不同的公共点,则这两个平面重合;③直线a,b,c,若a与b共面,b与c共面,则a与c共面;④若直线l上有一点在平面α外,则l在平面α外.其中错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,准线方程为
,准线方程为![]() ,直线
,直线![]() 过定点
过定点![]() (
(![]() )且与抛物线交于
)且与抛物线交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求抛物线的方程;
(2)![]() 是否为定值,若是,求出这个定值;若不是,请说明理由;
是否为定值,若是,求出这个定值;若不是,请说明理由;
(3)当![]() 时,设
时,设![]() ,记
,记![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对各老旧小区环境整治效果进行满意度测评,共有10000人参加这次测评(满分100分,得分全为整数).为了解本次测评分数情况,从中随机抽取了部分人的测评分数进行统计,整理见下表:
组别 | 分组 | 频数 | 频率 |
1 |
| 3 | 0.06 |
2 |
| 15 | 0.3 |
3 |
| 21 |
|
4 |
| 3 | 0.12 |
5 |
|
| 0.1 |
合计 |
| 1.00 | |
(1)求出表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若分数在80(含80分)以上表示对该项目“非常满意”,其中分数在90(含90分)以上表示“十分满意”,现从被抽取的“非常满意“人群中随机抽取2人,求至少有一人分数是“十分满意”的概率;
(3)请你根据样本数据估计全市的平均测评分数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com