
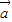 •(
•(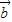 -
-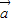 ),其中
),其中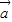 =(cosωx,0),
=(cosωx,0),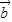 =(
=(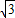 sinωx,1),且ω为正实数.
sinωx,1),且ω为正实数. 有且仅有一个交点,求ω的值,并求满足f(x)=
有且仅有一个交点,求ω的值,并求满足f(x)=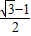 ,x∈[
,x∈[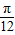 ,
,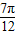 ]的x的值.
]的x的值.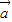 •(
•(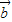 -
-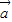 ),其中
),其中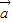 =(cosωx,0),
=(cosωx,0),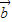 =(
=(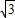 sinωx,1),求出函数的解析式,进而根据正弦型函数的图象和性质,可得函数的最大值;
sinωx,1),求出函数的解析式,进而根据正弦型函数的图象和性质,可得函数的最大值; 有且仅有一个交点,可得函数的周期为π,进而构造三角方程,求出x的值.
有且仅有一个交点,可得函数的周期为π,进而构造三角方程,求出x的值.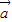 =(cosωx,0),
=(cosωx,0),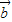 =(
=(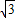 sinωx,1),
sinωx,1),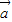 •(
•(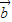 -
-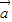 )=(cosωx,0)•(
)=(cosωx,0)•(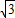 sinωx-cosωx,1)=
sinωx-cosωx,1)=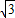 sinωx•cosωx-cosωx•cosωx
sinωx•cosωx-cosωx•cosωx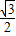 sin(2ωx)-
sin(2ωx)- cos(2ωx)-
cos(2ωx)- =sin(2ωx-
=sin(2ωx-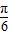 )-
)-


 )-
)- =
=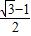
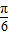 )=
)=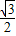
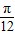 ,
,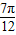 ]
]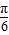 ∈[0,π]
∈[0,π]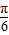 =
=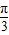 ,或2x-
,或2x-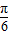 =
=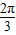
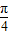 ,或x=
,或x=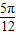


科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com