【题目】下面四个命题中真命题的是（ ）
①在回归分析模型中，残差平方和越大，说明模型的拟合效果越好；
②两个随机变量相关性越强，则相关系数的绝对值越接近于1；
③在回归直线方程
中，当解释变量
每增加一个单位时，预报变量平均增加0.4个单位；
④对分类变量
与
的随机变量
的观测值
来说，越小，“与有关系”的把握程度越大.
A.①④B.②④C.①③D.②③
【答案】D
【解析】
①根据回归分析基本思想判断，残差平方和越小，拟合效果越好；
②根据相关系数的计算公式，来判断②是否正确；
③利用回归方程的系数，判断③是否正确；
④根据独立性检验的基本思想，观测值
越大，“
与
有关系”的把握程度越大.
根据回归分析基本思想，残差平方和越大，说明模型的拟合效果越不好，即①为假命题；两个随机变量相关性越强，则相关系数的绝对值越接近于1；两个随机变量相关性越弱，则相关系数的绝对值越接近于0；故②为真命题；在回归直线方程
中，当解释变量
每增加一个单位时，预报变量平均增加0.4个单位，故③为真命题；对分类变量与的随机变量
的观测值
来说，越小，“与有关系”的把握程度越小，故④为假命题；故真命题为：②③.
故选：D.
科目：高中数学 来源： 题型：
【题目】如图所示四棱锥
的底面为正方形，
平面
则下列结论中不正确的是（ ）
A.
B.
平面
C.直线
与平面
所成的角等于30°D.SA与平面SBD所成的角等于SC与平面SBD所成的角
查看答案和解析>>
科目：高中数学 来源： 题型：
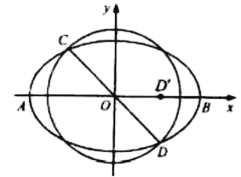
【题目】如图，已知AB为椭圆E：
（a＞b＞0）的长轴，过坐标原点O且倾斜角为135°的直线交椭圆E于C，D两点，且D在x轴上的射影D'恰为椭圆E的长半轴OB的中点．
（1）求椭圆E的离心率；
（2）若AB＝8，不过第四象限的直线l与椭圆E和以CD为直径的圆均相切，求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果数列
，
，…，
（m ≥ 3，
）满足：①＜＜…＜；②存在实数
，
，
，…，
和d，使得≤＜≤＜≤
＜…≤＜，且对任意0 ≤ i ≤ m﹣1（I 
），均有
，那么称数列，，…，是“Q数列”．
（1）判断数列1，3，6，10是不是“Q数列”，并说明理由；
（2）已知k，t均为常数，且k＞0，求证：对任意给定的不小于3的正整数m，数列
（n＝1，2，…，m）都是“Q数列”；
（3）若数列
（n＝1，2，…，m）是“Q数列”，求m的所有可能值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
为边长为2的菱形，
，
，面
面，点
为棱
的中点.
（1）在棱
上是否存在一点
，使得
面
，并说明理由；
（2）当二面角
的余弦值为
时，求直线
与平面所成的角.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市规定，高中学生在校期间须参加不少于80小时的社区服务才合格．某校随机抽取20位学生参加社区服务的数据，按时间段
（单位：小时）进行统计，其频率分布直方图如图所示．
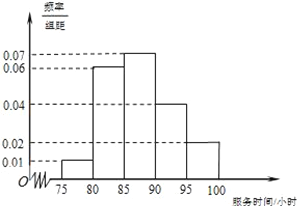
（1）求抽取的20人中，参加社区服务时间不少于90小时的学生人数；
（2）从参加社区服务时间不少于90小时的学生中任意选取2人，求所选学生的参加社区服务时间在同一时间段内的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥O﹣ABCD中，OA⊥底面ABCD，且底面ABCD是边长为2的正方形，且OA＝2，M，N分别为OA，BC的中点.
（1）求证：直线MN
平面OCD；
（2）求点B到平面DMN的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
