
【题目】在△ABC中,内角A、B、C的对边分别为a,b,c,且a>c,已知 ![]()
![]() =2,cosB=
=2,cosB= ![]() ,b=3,求:
,b=3,求:
(Ⅰ)a和c的值;
(Ⅱ)cos(B﹣C)的值.
【答案】解:(Ⅰ)∵ ![]()
![]() =2,cosB=
=2,cosB= ![]() , ∴cacosB=2,即ac=6①,
, ∴cacosB=2,即ac=6①,
∵b=3,
∴由余弦定理得:b2=a2+c2﹣2accosB,即9=a2+c2﹣4,
∴a2+c2=13②,
联立①②得:a=3,c=2;
(Ⅱ)在△ABC中,sinB= ![]() =
= 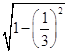 =
= ![]() ,
,
由正弦定理 ![]() =
= ![]() 得:sinC=
得:sinC= ![]() sinB=
sinB= ![]() ×
× ![]() =
= ![]() ,
,
∵a=b>c,∴C为锐角,
∴cosC= ![]() =
= 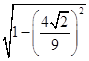 =
= ![]() ,
,
则cos(B﹣C)=cosBcosC+sinBsinC= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]()
【解析】(Ⅰ)利用平面向量的数量积运算法则化简 ![]()
![]() =2,将cosB的值代入求出ac=6,再利用余弦定理列出关系式,将b,cosB以及ac的值代入得到a2+c2=13,联立即可求出ac的值;(Ⅱ)由cosB的值,利用同角三角函数间基本关系求出sinB的值,由c,b,sinB,利用正弦定理求出sinC的值,进而求出cosC的值,原式利用两角和与差的余弦函数公式化简后,将各自的值代入计算即可求出值.
=2,将cosB的值代入求出ac=6,再利用余弦定理列出关系式,将b,cosB以及ac的值代入得到a2+c2=13,联立即可求出ac的值;(Ⅱ)由cosB的值,利用同角三角函数间基本关系求出sinB的值,由c,b,sinB,利用正弦定理求出sinC的值,进而求出cosC的值,原式利用两角和与差的余弦函数公式化简后,将各自的值代入计算即可求出值.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() :
:  (
(![]() 为参数)和直线
为参数)和直线![]() :
: ![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的方程化为普通方程;
的方程化为普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() 为弦
为弦![]() 的中点,求弦
的中点,求弦![]() 所在的直线方程.
所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(ax+1)+mx是偶函数.
(1)求m;
(2)当a>1时,若函数f(x)的图像与直线l:y=﹣mx+n无公共点,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷影长的记录中,冬至和夏至的晷影长是实测得到的,其他节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) | 惊蛰(寒露) | 春分(秋分) |
晷影长(寸) | 135 |
|
|
|
|
| 75.5 |
节气 | 清明(白露) | 谷雨(处暑) | 立夏(立秋) | 小满(大暑) | 芒种(小暑) | 夏至 | |
晷影长(寸) |
|
|
|
|
| 16.0 |
已知《易知》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为__________寸.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn . 已知a1=1, ![]() =an+1﹣
=an+1﹣ ![]() n2﹣n﹣
n2﹣n﹣ ![]() ,n∈N* .
,n∈N* .
(1)求数列{an}的通项公式;
(2)设数列{bn}满足an﹣an﹣1=bna ![]() ,求数列{bn}的n前项和Tn;
,求数列{bn}的n前项和Tn;
(3)是否存在实数λ,使得不等式λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com