
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源:不详 题型:解答题
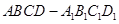 中,
中,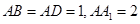 ,G是
,G是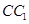 上的动点。
上的动点。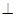
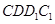 ;
;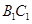 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;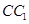 的中点,求二面角G-AD-C的大小;
的中点,求二面角G-AD-C的大小;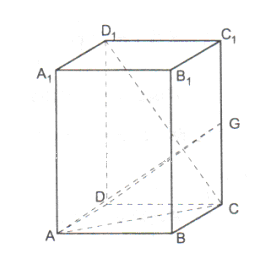
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
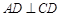 ,
,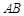 ∥
∥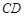 ,
,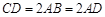 .
.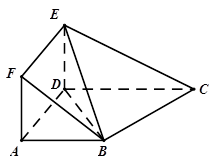
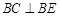 ;
; 与平面
与平面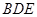 所成角的正切值;
所成角的正切值;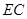 上找一点
上找一点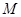 ,使得
,使得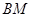 ∥平面ADEF,请确定M点的位置,并给出证明.
∥平面ADEF,请确定M点的位置,并给出证明.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
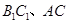 上,B1E=3EC1,AC=BC=CC1=4.
上,B1E=3EC1,AC=BC=CC1=4.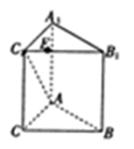
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.a//b, a⊥α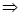 a⊥b a⊥b | B.a⊥α, b⊥α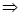 a//b a//b |
C.a⊥α, a⊥b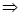 b//α b//α | D.a//α,a⊥b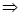 b⊥α b⊥α |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
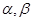 为平面,且m
为平面,且m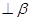 ,则“m//
,则“m//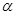 ”是“
”是“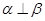 ”的充要条件;
”的充要条件;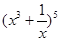 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;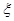 ~N(0,1),若P(
~N(0,1),若P(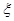 ≥2)=p,则P(-2<
≥2)=p,则P(-2<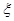 <0)=
<0)=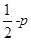 ;
;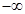 ,2);
,2);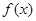 满足
满足 ,且0<x<
,且0<x<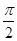 时
时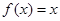 ,则函数
,则函数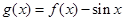 在[
在[ ,
,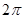 ]上有5个零点.
]上有5个零点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com