
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)设![]() 是函数
是函数![]() 的四个不同的零点,问是否存在实数
的四个不同的零点,问是否存在实数![]() ,使得其中三个零点成等差数列?若存在,求出所有
,使得其中三个零点成等差数列?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的上下焦点分别为F1 , F2 , 离心率为
的上下焦点分别为F1 , F2 , 离心率为 ![]() ,P为C上动点,且满足
,P为C上动点,且满足 ![]() |,△QF1F2面积的最大值为4. (Ⅰ)求Q点轨迹E的方程和椭圆C的方程;
|,△QF1F2面积的最大值为4. (Ⅰ)求Q点轨迹E的方程和椭圆C的方程;
(Ⅱ)直线y=kx+m(m>0)与椭圆C相切且与曲线E交于M,N两点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面凸四边形![]() 中(凸四边形指没有角度数大于
中(凸四边形指没有角度数大于![]() 的四边形),
的四边形),![]() .
.

(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)已知![]() ,记四边形
,记四边形![]() 的面积为
的面积为![]() .
.
① 求![]() 的最大值;
的最大值;
② 若对于常数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.(直接写结果,不需要过程)
的取值范围.(直接写结果,不需要过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|. (I)求不等式f(x)<|2x+1|﹣1的解集M;
(Ⅱ)设a,b∈M,证明:f(ab)>f(a)﹣f(﹣b).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 与直线
与直线![]() :
:![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.
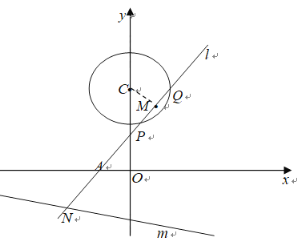
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,点M是PQ的中点,直线
两点,点M是PQ的中点,直线![]() 与直线
与直线![]() 相交于点N.探索
相交于点N.探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
(Ⅰ)证明:直线CE∥平面PAB;
(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 ![]() 的中点.(12分)
的中点.(12分)
(Ⅰ)设P是 ![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.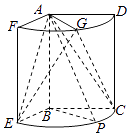
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名男生、3名女生站成一排:
(1)女生都不站在两端,有多少不同的站法?
(2)三名男生要相邻,有多少种不同的站法?
(3)三名女生互不相邻,三名男生也互不相邻,有多少种不同的站法?
(4)女生甲,女生乙都不与男生丙相邻,有多少种不同的站法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com