
【题目】已知椭圆C:![]() 的左焦点为
的左焦点为![]() ,且点
,且点![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 设点P关于x轴的对称点为点
设点P关于x轴的对称点为点![]() 不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若
不经过P点且斜率为k的直线l与C交于A,B两点,直线PA,PB分别与x轴交于点M,N,若![]() ,求k.
,求k.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
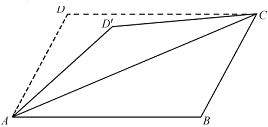
【题目】如图,四边形ABCD为矩形,沿AB将△ADC翻折成![]() .设二面角
.设二面角![]() 的平面角为
的平面角为![]() ,直线
,直线![]() 与直线BC所成角为
与直线BC所成角为![]() ,直线
,直线![]() 与平面ABC所成角为
与平面ABC所成角为![]() ,当
,当![]() 为锐角时,有
为锐角时,有
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,椭圆
,椭圆![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)当直线![]() 过右焦点
过右焦点![]() 时,求椭圆
时,求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点,且
为坐标原点,且![]() ,若点
,若点![]() 在以线段
在以线段![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司印制了一批文化衫,每件文化衫可有红、黄、蓝三种不同的颜色和四种不同的图案.现将这批文化衫分发给![]() 名新员工,每名员工恰好分到图案不同的4件.试求
名新员工,每名员工恰好分到图案不同的4件.试求![]() 的最小值,使得总存在两个人,他们所分到的某两种图案的4件文化衫的颜色全部相同.
的最小值,使得总存在两个人,他们所分到的某两种图案的4件文化衫的颜色全部相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市南澳县是广东唯一的海岛县,海区面积广阔,发展太平洋牡蛎养殖业具有得天独厚的优势,所产的“南澳牡蛎”是中国国家地理标志产品,产量高、肉质肥、营养好,素有“海洋牛奶精品”的美誉.根据养殖规模与以往的养殖经验,产自某南澳牡蛎养殖基地的单个“南澳牡蛎”质量(克)在正常环境下服从正态分布![]() .
.
(1)购买10只该基地的“南澳牡蛎”,会买到质量小于20g的牡蛎的可能性有多大?
(2)2019年该基地考虑增加人工投入,现有以往的人工投入增量x(人)与年收益增量y(万元)的数据如下:
人工投入增量x(人) | 2 | 3 | 4 | 6 | 8 | 10 | 13 |
年收益增量y(万元) | 13 | 22 | 31 | 42 | 50 | 56 | 58 |
该基地为了预测人工投入增量为16人时的年收益增量,建立了y与x的两个回归模型:
模型①:由最小二乘公式可求得y与x的线性回归方程:![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线:![]() 的附近,对人工投入增量x做变换,令
的附近,对人工投入增量x做变换,令![]() ,则
,则![]() ,且有
,且有 .
.

(i)根据所给的统计量,求模型②中y关于x的回归方程(精确到0.1);
(ii)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测人工投入增量为16人时的年收益增量.
,并选择拟合精度更高、更可靠的模型,预测人工投入增量为16人时的年收益增量.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
附:若随机变量![]() ,则
,则![]() ,
,![]() ;
;
样本![]() 的最小二乘估计公式为:
的最小二乘估计公式为: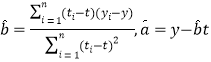 ,
,
另,刻画回归效果的相关指数
查看答案和解析>>
科目:高中数学 来源: 题型:
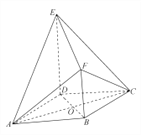
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 、
、![]() 为大于3的整数,将
为大于3的整数,将![]() 的立方体分割为
的立方体分割为![]() 个单位正方体,从一角的单位正方体起第
个单位正方体,从一角的单位正方体起第![]() 层、第
层、第![]() 行、第
行、第![]() 列的单位正方体记为
列的单位正方体记为![]() .求所有有序六元数组
.求所有有序六元数组![]() 的个数,使得一只蚂蚁从
的个数,使得一只蚂蚁从![]() 出发,经过每个小正方体恰一次到达
出发,经过每个小正方体恰一次到达![]() .(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
.(注)蚂蚁可以从一个单位正方体爬到另一个与之有公共面的相邻正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com