
分析 (1)由PF1+PF2=4得PF1•PF2=PF1(4-PF1)=-(PF1-2)2+4,从而求最值;
(2)化简${PF}_{1}^{2}{+PF}_{2}^{2}$=(PF1+PF2)2-2PF1•PF2=16-2PF1•PF2,从而求最小值;
(3)由余弦定理可得cos∠F1PF2=$\frac{P{{F}_{1}}^{2}+P{{F}_{2}}^{2}-{F}_{1}{{F}_{2}}^{2}}{2P{F}_{1}P{F}_{2}}$=$\frac{2}{P{F}_{1}P{F}_{2}}$-1,从而求角的最大值;
(4)PF1的最大值为2+$\sqrt{3}$,最小值为2-$\sqrt{3}$.
解答 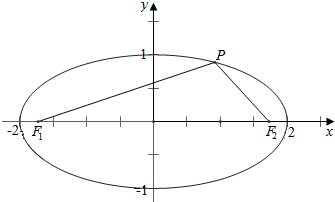 解:(1)∵PF1+PF2=4,∴PF2=4-PF1,
解:(1)∵PF1+PF2=4,∴PF2=4-PF1,
∴PF1•PF2=PF1(4-PF1)
=-(PF1-2)2+4,
∵a-c=2-$\sqrt{3}$≤PF1≤2+$\sqrt{3}$=a+c,
∴1≤-(PF1-2)2+4≤4,
∴PF1•PF2的最大值为4,最小值为1;
(2)∵${PF}_{1}^{2}{+PF}_{2}^{2}$
=(PF1+PF2)2-2PF1•PF2
=16-2PF1•PF2,
∵PF1•PF2的最大值为4,
∴${PF}_{1}^{2}{+PF}_{2}^{2}$的最小值为16-8=8;
(3)∵cos∠F1PF2=$\frac{P{{F}_{1}}^{2}+P{{F}_{2}}^{2}-{F}_{1}{{F}_{2}}^{2}}{2P{F}_{1}P{F}_{2}}$
=$\frac{(P{F}_{1}+P{F}_{2})^{2}-{F}_{1}{{F}_{2}}^{2}-2P{F}_{1}P{F}_{2}}{2P{F}_{1}P{F}_{2}}$
=$\frac{2}{P{F}_{1}P{F}_{2}}$-1,
故当PF1•PF2取得最大值4时,
cos∠F1PF2有最小值-$\frac{1}{2}$,
故∠F1PF2的最大值为$\frac{2π}{3}$.
(4)PF1的最大值为2+$\sqrt{3}$,最小值为2-$\sqrt{3}$.
点评 本题考查了椭圆的基本性质的应用及配方法的应用,同时考查了余弦定理的应用及数形结合的思想应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{π}{2}]$ | B. | $[0,\frac{π}{3}],[\frac{5π}{6},π]$ | C. | $[\frac{π}{3},\frac{5π}{6}]$ | D. | $[\frac{π}{2},π]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
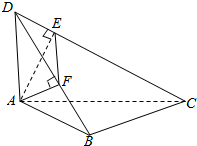 如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.
如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p=-1,q=6 | B. | p=1,q=6 | C. | p=-1,q=-6 | D. | p=1,q=-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com