
【题目】已知曲线C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (
(![]() 为参数,0≤α<π).
为参数,0≤α<π).
(1)求曲线C的直角坐标方程.并说明曲线C的形状;
(2)若直线l经过点M(1,0)且与曲线C交于A、B两点,求|AB|.
【答案】(1)y2=4x,曲线C是抛物线.(2)8
【解析】
(1)运用x=ρcosθ,y=ρsinθ,即可将曲线C的极坐标方程化为直角坐标方程;
(2)化直线的参数方程为普通方程,再由条件,即可得到斜率,再联立抛物线方程,消去x,得到y的方程,运用韦达定理和弦长公式,即可得到所求值.
解:(1)对于曲线C:![]() 可化为
可化为![]() ,
,
把互化公式代入,得y=![]() ,
,
∴曲线C的直角坐标方程为y2=4x,
曲线C是抛物线.
(2)根据条件直线l经过两定点(1,0)和(0,1),
∴其方程为x+y=1.
由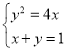 ,消去x并整理得:y2+4y-4=0,
,消去x并整理得:y2+4y-4=0,
令A(x1,y1),B(x2,y2),
则y1+y2=-4,y1y2=-4,
∴|AB|=![]()
![]() =
=![]() =8
=8


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙两个学生在高二的6次数学测试的成绩(百分制)制成如图所示的茎叶图,进入高三后,由于改进了学习方法,甲、乙这两个学生的考试成绩预计同时有了大的提升:若甲(乙)的高二任意一次考试成绩为![]() ,则甲(乙)的高三对应的考试成绩预计为
,则甲(乙)的高三对应的考试成绩预计为![]() .
.

(1)试预测:高三6次测试后,甲、乙两个学生的平均成绩分别为多少?谁的成绩更稳定?
(2)若已知甲、乙两个学生的高二6次考试成绩分别由低到高进步的,定义![]() 为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求
为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求![]() 的平均值.
的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他门各应偿还多少?该问题中,1斗为10升,则羊主人应偿还多少升粟?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行象棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)(x∈R)满足f(1+x)=f(1-x)且x∈[-1,1]时,f(x)=1-x2,函数g(x)=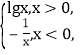 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com