
ЁОЬтФПЁПФГбЇаЃЩЯбЇЦкЕФЦкжаПМЪдКѓЃЌЮЊСЫСЫНтФГбЇПЦЕФПМЪдГЩМЈЃЌИљОнбЇЩњЕФПМЪдГЩМЈРћгУЗжВуГщбљГщШЁ![]() УћбЇЩњЕФГЩМЈНјааЭГМЦЃЈЫљгабЇЩњГЩМЈОљВЛЕЭгк
УћбЇЩњЕФГЩМЈНјааЭГМЦЃЈЫљгабЇЩњГЩМЈОљВЛЕЭгк![]() ЗжЃЉЃЌЕУЕНбЇЩњГЩМЈЕФЦЕТЪЗжВМжБЗНЭМШчЭМЃЌЛиД№ЯТСаЮЪЬтЃЛ
ЗжЃЉЃЌЕУЕНбЇЩњГЩМЈЕФЦЕТЪЗжВМжБЗНЭМШчЭМЃЌЛиД№ЯТСаЮЪЬтЃЛ
ЃЈЂёЃЉИљОнЦЕТЪЗжВМжБЗНЭММЦЫуБОДЮПМЪдГЩМЈЕФЦНОљЗжЃЛ
ЃЈЂђЃЉвбжЊБОДЮШЋаЃПМЪдГЩМЈдк![]() ФкЕФШЫЪ§ЮЊ
ФкЕФШЫЪ§ЮЊ![]() ЃЌЪдШЗЖЈШЋаЃЕФзмШЫЪ§ЃЛ
ЃЌЪдШЗЖЈШЋаЃЕФзмШЫЪ§ЃЛ
ЃЈЂѓЃЉШєБОДЮПМЪдГщВщЕФ![]() ШЫжаПМЪдГЩМЈдк
ШЫжаПМЪдГЩМЈдк![]() ФкЕФга
ФкЕФга![]() УћХЎЩњЃЌЦфгрЮЊФаЩњЃЌДгжабЁдёСНУћбЇЩњЃЌЧѓбЁдёвЛУћФаЩњгывЛУћХЎЩњЕФИХТЪ.
УћХЎЩњЃЌЦфгрЮЊФаЩњЃЌДгжабЁдёСНУћбЇЩњЃЌЧѓбЁдёвЛУћФаЩњгывЛУћХЎЩњЕФИХТЪ.

ЁОД№АИЁПЃЈ1ЃЉ75ЃЈ2ЃЉ1050ЃЈ3ЃЉ![]()
ЁОНтЮіЁПЁОЪдЬтЗжЮіЁПЃЈЃБЃЉНшжњЦЕТЪЗжВМжБЗНЭМЩЯУцЕФЪ§ОндЫгУМгШЈЦНОљЪ§ЙЋЪНЧѓНтЃЛЃЈЃВЃЉдЫгУЦЕТЪКЭЦЕЪ§жЎМфЕФЙиЯЕЧѓНтЃЛЃЈЃГЃЉдЫгУСаОйЗЈКЭЙХЕфИХаЭЕФМЦЫуЙЋЪНЧѓНтЃК
ЃЈЂёЃЉИљОнЦЕТЪЗжВМжБЗНЭМПЩжЊЃЌБОДЮПМЪдГЩМЈЕФЦНОљЗжЮЊ
![]() ЃЈЗжЃЉ.
ЃЈЗжЃЉ.
ЃЈЂђЃЉБОДЮШЋаЃПМЪдГЩМЈдк![]() ЗжвдЯТЕФЦЕТЪЮЊ
ЗжвдЯТЕФЦЕТЪЮЊ![]() ЃЌЫљвдШЋаЃЕФзмШЫЪ§ЮЊ
ЃЌЫљвдШЋаЃЕФзмШЫЪ§ЮЊ![]() .
.
ЃЈЂѓЃЉИљОнЦЕТЪЗжВМжБЗНЭМПЩжЊЃЌПМЪдГЩМЈдк![]() ФкЕФбЇЩњШЫЪ§ЮЊ
ФкЕФбЇЩњШЫЪ§ЮЊ![]() ЃЌдђга
ЃЌдђга![]() УћФаЩњ.
УћФаЩњ.
ЩшФаЩњЗжБ№ЮЊ![]() ЃЌХЎЩњЗжБ№ЮЊ
ЃЌХЎЩњЗжБ№ЮЊ![]() ЃЌЫљгаЧщПіга
ЃЌЫљгаЧщПіга
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЙВ15жжЃЌ
ЃЌЙВ15жжЃЌ
ЦфжавЛУћФаЩњгывЛУћХЎЩњЕФЧщПіга![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЙВ8жжЃЌЙЪЫљЧѓИХТЪЮЊ
ЃЌЙВ8жжЃЌЙЪЫљЧѓИХТЪЮЊ![]() .
.


 ПМЧАБиСЗЯЕСаД№АИ
ПМЧАБиСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвд
жаЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎШєжБЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎШєжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌЧњЯп
ЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌНЋЧњЯп
ЃЌНЋЧњЯп![]() ЩЯЫљгаЕуЕФКсзјБъЫѕЖЬЮЊдРДЕФвЛАыЃЌзнзјБъВЛБфЃЌШЛКѓдйЯђгвЦНвЦвЛИіЕЅЮЛЕУЕНЧњЯп
ЩЯЫљгаЕуЕФКсзјБъЫѕЖЬЮЊдРДЕФвЛАыЃЌзнзјБъВЛБфЃЌШЛКѓдйЯђгвЦНвЦвЛИіЕЅЮЛЕУЕНЧњЯп![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈЂђЃЉвбжЊжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИїЪНЃК
ЃЈ1ЃЉвбжЊloga ![]() ЃМ1ЃЌдђaЃО
ЃМ1ЃЌдђaЃО ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉКЏЪ§y=2xЕФЭМЯѓгыКЏЪ§y=2ЉxЕФЭМЯѓЙигкyжсЖдГЦЃЛ
ЃЈ3ЃЉКЏЪ§fЃЈxЃЉ=lgЃЈmx2+mx+1ЃЉЕФЖЈвхгђЪЧRЃЌдђmЕФШЁжЕЗЖЮЇЪЧ0ЁмmЃМ4ЃЛ
ЃЈ4ЃЉКЏЪ§y=lnЃЈЉx2+xЃЉЕФЕндіЧјМфЮЊЃЈЉЁоЃЌ ![]() ]
]
е§ШЗЕФга ЃЎ ЃЈАбФуШЯЮЊе§ШЗЕФађКХШЋВПаДЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЇУПШеЩњВњвЛжжДѓаЭВњЦЗ1МўЃЌУПМўВњЦЗЕФЭЖШыГЩБОЮЊ2000дЊ.ВњЦЗжЪСПЮЊвЛЕШЦЗЕФИХТЪЮЊ![]() ЃЌЖўЕШЦЗЕФИХТЪЮЊ
ЃЌЖўЕШЦЗЕФИХТЪЮЊ![]() ЃЌУПМўвЛЕШЦЗЕФГіГЇМлЮЊ10000дЊЃЌУПМўЖўЕШЦЗЕФГіГЇМлЮЊ8000дЊ.ШєВњЦЗжЪСПВЛФмДяЕНвЛЕШЦЗЛђЖўЕШЦЗЃЌГ§ГЩБОВЛФмЪеЛиЭтЃЌУЛЩњВњвЛМўВњЦЗЛЙЛсДјРД1000дЊЕФЫ№ЪЇ.
ЃЌУПМўвЛЕШЦЗЕФГіГЇМлЮЊ10000дЊЃЌУПМўЖўЕШЦЗЕФГіГЇМлЮЊ8000дЊ.ШєВњЦЗжЪСПВЛФмДяЕНвЛЕШЦЗЛђЖўЕШЦЗЃЌГ§ГЩБОВЛФмЪеЛиЭтЃЌУЛЩњВњвЛМўВњЦЗЛЙЛсДјРД1000дЊЕФЫ№ЪЇ.
ЃЈ1ЃЉЧѓдкСЌајЩњВњ3ЬьжаЃЌЧЁгавЛЬьЩњВњЕФСНМўВњЦЗЖМЮЊвЛЕШЦЗЕФЕФИХТЪЃЛ
ЃЈ2ЃЉвбжЊИУГЇФГШеЩњВњЕФ2МўВњЦЗжагавЛМўЮЊвЛЕШЦЗЃЌЧѓСэвЛМўвВЮЊвЛЕШЦЗЕФИХТЪЃЛ
ЃЈ3ЃЉЧѓИУГЇУПШеЩњВњИУжжВњЦЗЫљЛёЕУЕФРћШѓ![]() ЃЈдЊЃЉЕФЗжВМСаМАЪ§бЇЦкЭћ.
ЃЈдЊЃЉЕФЗжВМСаМАЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=log4ЃЈ4x+1ЃЉ+kxЃЈkЁЪRЃЉЪЧХМКЏЪ§ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§kЕФжЕЃЛ
ЃЈ2ЃЉЩшgЃЈxЃЉ=log4ЃЈa2x+aЃЉЃЌШєfЃЈxЃЉ=gЃЈxЃЉгаЧвжЛгавЛИіЪЕЪ§НтЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГДѓбЇСЊУЫЕФзджїеаЩњПМЪджаЃЌБЈПМЮФЪЗзЈвЕЕФПМЩњВЮМгСЫШЫЮФЛљДЁбЇПЦПМЪдПЦФПЁАгяЮФЁБКЭЁАЪ§бЇЁБЕФПМЪд.ФГПМГЁПМЩњЕФСНПЦПМЪдГЩМЈЪ§ОнЭГМЦШчЯТЭМЫљЪОЃЌБОДЮПМЪджаГЩМЈдк![]() ФкЕФМЧЮЊ
ФкЕФМЧЮЊ![]() ЃЌЦфжаЁАгяЮФЁБПЦФПГЩМЈдк
ЃЌЦфжаЁАгяЮФЁБПЦФПГЩМЈдк![]() ФкЕФПМЩњга10ШЫ.
ФкЕФПМЩњга10ШЫ.
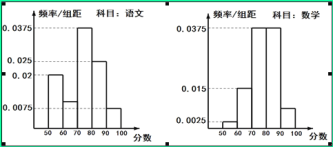
ЃЈ1ЃЉЧѓИУПМГЁПМЩњЪ§бЇПЦФПГЩМЈЮЊ![]() ЕФШЫЪ§ЃЛ
ЕФШЫЪ§ЃЛ
ЃЈ2ЃЉвбжЊВЮМгБОПМГЁВтЪдЕФПМЩњжаЃЌЧЁга2ШЫЕФСНПЦГЩМЈОљЮЊ![]() .дкжСЩйвЛПЦГЩМЈЮЊ
.дкжСЩйвЛПЦГЩМЈЮЊ![]() ЕФПМЩњжаЃЌЫцЛњГщШЁ2ШЫНјааЗУЬИЃЌЧѓет2ШЫЕФСНПЦГЩМЈОљЮЊ
ЕФПМЩњжаЃЌЫцЛњГщШЁ2ШЫНјааЗУЬИЃЌЧѓет2ШЫЕФСНПЦГЩМЈОљЮЊ![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§fЃЈxЃЉ=ax2+bx+cЃЈaЁй0ЃЉЃЌМЧf[2]ЃЈxЃЉ=fЃЈfЃЈxЃЉЃЉЃЌР§ЃКfЃЈxЃЉ=x2+1ЃЌ
дђf[2]ЃЈxЃЉ=ЃЈfЃЈxЃЉЃЉ2+1=ЃЈx2+1ЃЉ2+1ЃЛ
ЃЈ1ЃЉfЃЈxЃЉ=x2ЉxЃЌНтЙигкxЕФЗНГЬf[2]ЃЈxЃЉ=xЃЛ
ЃЈ2ЃЉМЧЁї=ЃЈbЉ1ЃЉ2Љ4acЃЌШєf[2]ЃЈxЃЉ=xгаЫФИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓЁїЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЧЪа100ЛЇОгУёЕФдТЦНОљгУЕчСП(ЕЅЮЛ:ЖШ),вд[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]ЗжзщЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.

(1)ЧѓжБЗНЭМжаxЕФжЕ;
(2)ЧѓдТЦНОљгУЕчСПЕФжкЪ§КЭжаЮЛЪ§;
(3)дкдТЦНОљгУЕчСПЮЊ[220,240),[240,260),[260,280),[280,300]ЕФЫФзщгУЛЇжа,гУЗжВуГщбљЕФЗНЗЈГщШЁ11ЛЇОгУё,дђдТЦНОљгУЕчСПдк[220,240)ЕФгУЛЇжагІГщШЁЖрЩйЛЇ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшa=log36ЃЌa=log510ЃЌa=log714ЃЌдђЃЈ ЃЉ
A.aЃОbЃОc
B.aЃОcЃОb
C.cЃОaЃОb
D.cЃОbЃОa
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com