
【题目】已知椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,试探究:直线
,试探究:直线![]() 是否过定点,若是,求该定点的坐标,若不是,请说明.
是否过定点,若是,求该定点的坐标,若不是,请说明.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 过定点
过定点![]() .
.
【解析】
(1)由题意知直线![]() 的方程为
的方程为![]() , 由直线
, 由直线![]() 与圆
与圆![]() 相切,得
相切,得![]() 进而求解方程。
进而求解方程。
(2)证法一:由![]() 知,设直线
知,设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .联立
.联立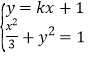 ,整理得
,整理得![]() ,求解点
,求解点![]() ,点
,点![]() ,进而表示出直线方程求解。
,进而表示出直线方程求解。
(1)圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]()
由题意知![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由直线![]() 与圆
与圆![]() 相切,得
相切,得![]() ,
,
解得![]() ,
,![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)证法一:由![]() 知
知![]() ,从而直线
,从而直线![]() 与坐标轴不垂直,故可设直线
与坐标轴不垂直,故可设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
联立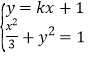 ,整理得
,整理得![]() ,
,
解得![]() 或
或![]() ,故点
,故点![]() 的坐标为
的坐标为![]() ,
,
同理,点![]() 的坐标为
的坐标为![]() ,
,
∴直线![]() 的斜率为
的斜率为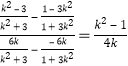 ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
所以直线![]() 过定点
过定点![]() .
.
证法二:由![]() ,知
,知![]() ,从而直线
,从而直线![]() 与
与![]() 轴不垂直,故可设直线
轴不垂直,故可设直线![]() 的方程为
的方程为![]() ,
,
联立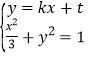 ,整理得
,整理得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,(*)
,(*)
由![]() 得
得![]() .
.
由![]() ,
,
得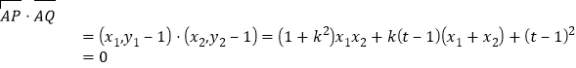 ,
,
将(*)代入,得![]() ,
,
所以直线![]() 过定点
过定点![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系x-O-y中,已知曲线E:![]() (t为参数)
(t为参数)
(1)在极坐标系O-x中,若A、B、C为E上按逆时针排列的三个点,△ABC为正三角形,其中A点的极角θ=![]() ,求B、C两点的极坐标;
,求B、C两点的极坐标;
(2)在直角坐标系x-O-y中,已知动点P,Q都在曲线E上,对应参数分别为t=α与t=2α (0<α<2π),M为PQ的中点,求 |MO| 的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
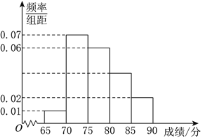
【题目】某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90)内)分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90).得到频率分布直方图如图C34.
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组学生中用分层抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬传统文化,某市举办了“高中生诗词大赛”,现从全市参加比赛的学生中随机抽取![]() 人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为
人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() .
.
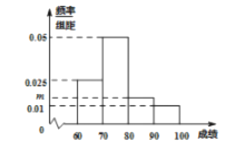
(1)求频率分布直方图中![]() 的值;
的值;
(2)在所抽取的![]() 名学生中,用分层抽样的方法在成绩为
名学生中,用分层抽样的方法在成绩为![]() 的学生中抽取了一个容量为
的学生中抽取了一个容量为![]() 的样本,再从该样本中任意抽取
的样本,再从该样本中任意抽取![]() 人,求
人,求![]() 人的成绩均在区间
人的成绩均在区间![]() 内的概率;
内的概率;
(3)若该市有![]() 名高中生参赛,根据此次统计结果,试估算成绩在区间
名高中生参赛,根据此次统计结果,试估算成绩在区间![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100![]() ,水温
,水温![]() 与时间
与时间![]() 近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度
近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度![]() 与时间
与时间![]() 近似满足函数的关系式为
近似满足函数的关系式为 ![]() (
(![]() 为常数), 通常这种热饮在40
为常数), 通常这种热饮在40![]() 时,口感最佳,某天室温为
时,口感最佳,某天室温为![]() 时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为

A. 35![]() B. 30
B. 30![]()
C. 25![]() D. 20
D. 20![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com