练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．抛掷一枚均匀的正方体骰子，向上的点数是奇数为事件A，事件A的对立事件是向上的点数是偶数．

    分析 抛掷一枚均匀的正方体骰子，向上的点数是奇数或偶数，即可得出结论．

    解答 解：抛掷一枚均匀的正方体骰子，向上的点数是奇数或偶数，
    向上的点数是奇数为事件A，事件A的对立事件是向上的点数是偶数，
    故答案为向上的点数是偶数．

    点评 本题考查对立事件，考查学生对概念的理解，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．已知△ABC中，AB=2，AC=3，tan∠BAC=2$\sqrt{2}$，D是BC边上的点，且BD=3CD，则$\overrightarrow{AD}•\overrightarrow{BC}$=$\frac{19}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

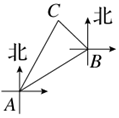    8．如图，某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发，沿北偏东60°方向进行海面巡逻，当航行半小时到达B处时，发现北偏西45°方向有一艘船C，若船C位于A的北偏东30°方向上，则缉私艇所在的B处与船C的距离是（　　）km．
    A．5（$\sqrt{6}$+$\sqrt{2}$）B．5（$\sqrt{6}$-$\sqrt{2}$）C．10（$\sqrt{6}$+$\sqrt{2}$）D．10（$\sqrt{6}$-$\sqrt{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设f（x）=|x-3|+|x-4|．
    （1）解不等式f（x）≤2；
    （2）已知实数x、y、z满足2x2+3y2+6z2=a（a＞0），且x+y+z的最大值是1，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．下列值为2的积分是（　　）
    A．$\int_0^5{（{2x-4}）dx}$B．$\int_0^π{cosxdx}$C．$\int_1^3{\frac{1}{x}dx}$D．$\int_0^π{sinxdx}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．如图，在△ABC中，点D满足$\overrightarrow{AD}$+2$\overrightarrow{BD}$=0，$\overrightarrow{CD}$•$\overrightarrow{AC}$=0，且|$\overrightarrow{CA}$+$\overrightarrow{AD}$|=2，则$\overrightarrow{DC}$•$\overrightarrow{CB}$=（　　）
    A．-6B．6C．2D．-$\frac{8}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知抛物线C：y2=4x，直线x=ny+4与抛物线C交于A，B两点．
    （Ⅰ）求证：$\overrightarrow{OA}$•$\overrightarrow{OB}$=0（其中O为坐标原点）；
    （Ⅱ）设F为抛物线C的焦点，直线l1为抛物线C的准线，直线l2是抛物线C的通径所在的直线，过C上一点P（x0，y0）（y0≠0）作直线l：y0y=2（x+x0）与直线l2相交于点M，与直线l1相交于点N，证明：点P在抛物线C上移动时，$\frac{|MF|}{|NF|}$恒为定值，并求出此定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知函数y=2sin（x+$\frac{π}{2}$）cos（x-$\frac{π}{2}$）与直线y=$\frac{1}{2}$相交，若在y轴右侧的交点自左向右依次记为M1，M2，M3，…，则|$\overrightarrow{{M}_{1}{M}_{12}}$|等于（　　）
    A．$\frac{16π}{3}$B．6πC．$\frac{17π}{3}$D．12π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在集合{x|0≤x≤a，a＞0}中随机取一个实数m，若|m|＜2的概率为$\frac{1}{3}$，则实数a的值为（　　）
    A．5B．6C．9D．12

    查看答案和解析>>

    同步练习册答案