
【题目】将一颗质地均匀的骰子先后抛掷2次,观察其向上的点数,分别记为x,y.
(1)若记“x+y=8”为事件A,求事件A发生的概率;
(2)若记“x2+y2≤12”为事件B,求事件B发生的概率.
【答案】
(1)解:将骰子抛掷一次,它出现的点数有1,2,3,4,5,6这六种结果.先后抛掷2次骰子,第一次骰子向上的点数有6种可能的结果,对于每一种,第二次又有6种可能出现的结果,于是基本事件一共有6×6=36(种)
记“x+y=8”为事件A,则A事件发生的基本事件有5个,所以所求的概率为 ![]()
(2)解:记“x2+y2≤12”为事件B,则B事件发生的基本事件有6个,所以所求的概率为 ![]()
答:事件A发生的概率为 ![]() ,事件B发生的概率为
,事件B发生的概率为 ![]()
【解析】(1)先后抛掷2次骰子,第一次骰子向上的点数有6种可能的结果,对于每一种,第二次又有6种可能出现的结果,于是基本事件一共有6×6=36(种),求出事件A的个数,即可求事件A发生的概率;(2)若记“x2+y2≤12”为事件B,求出事件B的个数,即可求事件B发生的概率.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]()
(1) 求点P的轨迹方程;
(2)设点![]() 在直线x=-3上,且
在直线x=-3上,且![]() .证明过点P且垂直于OQ的直线l过C的左焦点F.
.证明过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1=a,an+1=can+1﹣c(n∈N*),其中a,c为实数,且c≠0. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为公差不为0的等差数列{an}的前n项和,且a1=1,S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关系式中正确的是( )
A.sin 11°<cos 10°<sin 168°
B.sin 168°<sin 11°<cos 10°
C.sin 11°<sin 168°<cos 10°
D.sin 168°<cos 10°<sin 11°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心M在x轴上,半径为1,直线 ![]() ,被圆M所截的弦长为
,被圆M所截的弦长为 ![]() ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.
(I)求圆M的方程;
(II)设A(0,t),B(0,t+6)(﹣5≤t≤﹣2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),动点E满足直线EA与直线EB的斜率之积为﹣
,0),动点E满足直线EA与直线EB的斜率之积为﹣ ![]() .
.
(1)求动点E的轨迹C的方程;
(2)设过点F(1,0)的直线l1与曲线C交于点P,Q,记点P到直线l2:x=2的距离为d. 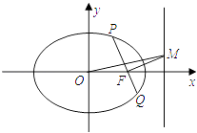
(ⅰ)求 ![]() 的值;
的值;
(ⅱ)过点F作直线l1的垂线交直线l2于点M,求证:直线OM平分线段PQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com