Question

20．给出下列命题 （1）${log_{0.5}}3＜{2^{\frac{1}{3}}}＜{（\frac{1}{3}）^{0.2}}$；
（2）函数f（x）=log₄x-2sinx有5个零点；
（3）函数f（x）=ln$\frac{x-4}{x-6}$+$\frac{x}{12}$的图象以$（5，\frac{5}{12}）$为对称中心；
（4）已知a＞0，b＞0，函数y=2ae^x+b的图象过点（0，1），则$\frac{1}{a}+\frac{1}{b}$的最小值是4$\sqrt{2}$．
其中正确命题的个数是（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 （1）利用指数函数和对数函数的图象和性质，判断三个式子的大小，可判断（1）；数形结合分析函数零点的个数，可判断（2）；构造函数g（x）=f（x+5）-$\frac{5}{12}$，并判断其奇偶性，结合函数图象的平移变换法则，可判断（3）；结合指数函数的图象和性质及基本不等式，可判断（4）．

解答 解：（1）∵log_0.53＜0，${2}^{\frac{1}{3}}＞1$，$0＜{（\frac{1}{3}）}^{0.2}＜1$，
故$lo{g}_{0.5}3＜{（\frac{1}{3}）}^{0.2}＜{2}^{\frac{1}{3}}$，故（1）错误；
（2）函数y=log₄x与y=2sinx的图象如下图所示：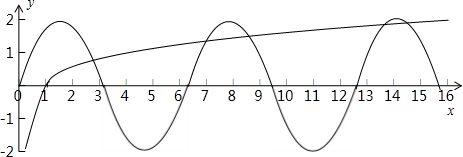

由图可得：函数y=log₄x与y=2sinx的图象有5个交点，故函数f（x）=log₄x-2sinx有5个零点，故（2）正确；
（3）令g（x）=f（x+5）-$\frac{5}{12}$=[ln$\frac{（x+5）-4}{（x+5）-6}$+$\frac{（x+5）}{12}$]-$\frac{5}{12}$=ln$\frac{x+1}{x-1}$+$\frac{x}{12}$，
则g（-x）=ln$\frac{-x+1}{-x-1}$-$\frac{x}{12}$=-（ln$\frac{x+1}{x-1}$+$\frac{x}{12}$）=-g（x），
故g（x）为奇函数，其图象关于原点对称，故函数f（x）=ln$\frac{x-4}{x-6}$+$\frac{x}{12}$的图象以$（5，\frac{5}{12}）$为对称中心，故（3）正确；
（4）已知a＞0，b＞0，函数y=2ae^x+b的图象过点（0，1），
则2a+b=1，则$\frac{1}{a}+\frac{1}{b}$=（$\frac{1}{a}+\frac{1}{b}$）（2a+b）=3+（$\frac{b}{a}$+$\frac{2a}{b}$）≥3+2$\sqrt{\frac{b}{a}•\frac{2a}{b}}$=3+2$\sqrt{2}$，
即$\frac{1}{a}+\frac{1}{b}$的最小值是3+2$\sqrt{2}$，故（4）错误．
故正确的命题的个数是2个，
故选：B

点评 本题以命题的真假判断与应用为载体，考查了函数的对称性，基本不等式，函数的零点，指数函数与对数函数的单调性等知识点，难度中档．