Question

在各项均为正数的等比数列{a_n}中，已知a₂=2a₁+3，且3a₂，a₄，5a₃成等差数列．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n=log₃a_n，求数列{a_nb_n}的前n项和S_n．

Answer 1

解：（Ⅰ）设数列{a_n}的公比为q，由题意得q＞0，
且即
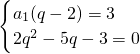
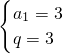
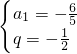
解得或（舍去），
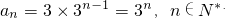
所以数列{a_n}的通项公式为． …（6分）
（Ⅱ）由（Ⅰ）可得b_n=log₃a_n=n，所以．
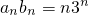
所以，
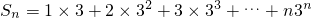
所以，
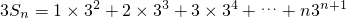
两式相减得==，
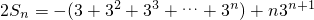
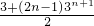
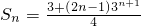
即． …（12分）
分析：（Ⅰ）根据已知条件建立等式，转化成首项和公比，解之即可求出所求；
（II）先求出数列{a_nb_n}的通项公式，根据通项公式的特点利用错位相消法进行求和，从而求出所求．
点评：本题主要考查了等比数列的通项公式，以及利用错位相消法进行求和，同时考查了计算能力，属于基础题．