
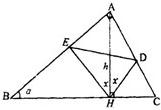
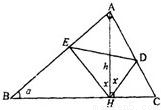
 如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.
如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积. | π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| h | ||
sin(
|
| EH | ||
sin(
|
| hcosα |
| cos(α-x) |
| hsinα |
| sin(α+x) |
| 1 |
| 2 |
| 1 |
| 2 |
| hcosα |
| cos(α-x) |
| hsinα |
| sin(α+x) |
| 1 |
| 2 |
| ||
|
| 1 |
| 4 |
| sin 22α |
| sin2α+sin2x |
| π |
| 4 |
| 1 |
| 4 |
| sin 22α |
| sin2α+1 |
| π |
| 4 |
| 1 |
| 4 |
| sin 22α |
| sin2α+1 |


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
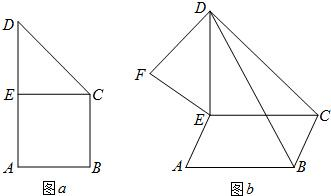 如图a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=
如图a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
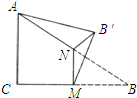 如图∠C=90°,AC=BC,M,N分别为BC和AB的中点,沿直线MN将△BMN折起,使二面角B'-MN-B为60°,则斜线B'A与平面ABC所成角的正切值为
如图∠C=90°,AC=BC,M,N分别为BC和AB的中点,沿直线MN将△BMN折起,使二面角B'-MN-B为60°,则斜线B'A与平面ABC所成角的正切值为
| ||
| 5 |
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
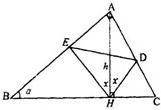 如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.
如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第3章 三角函数与三角恒等变换):3.14 三角最值问题(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com