
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 6 | m | -4 | -6 | -6 | -4 | n | 6 |
| A. | (-3,-1)和(-1,1) | B. | (-3,-1)和(2,4) | C. | (-1,1)和(1,2) | D. | (-∞,-3)和(4,+∞) |
 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某高校青年志愿者协会,组织大一学生开展一次爱心包裹劝募活动,将派出的志愿者,分成甲、乙两个小组,分别在两个不同的场地进行劝募,每个小组各6人,爱心人士每捐购一个爱心包裹,志愿者就将送出一个钥匙扣作为纪念,茎叶图记录了这两个小组成员某天劝募包裹时送出钥匙扣的个数,且图中乙组的一个数据模糊不清,用x表示,已知甲组送出钥匙扣的平均数比乙组的平均数少一个.
某高校青年志愿者协会,组织大一学生开展一次爱心包裹劝募活动,将派出的志愿者,分成甲、乙两个小组,分别在两个不同的场地进行劝募,每个小组各6人,爱心人士每捐购一个爱心包裹,志愿者就将送出一个钥匙扣作为纪念,茎叶图记录了这两个小组成员某天劝募包裹时送出钥匙扣的个数,且图中乙组的一个数据模糊不清,用x表示,已知甲组送出钥匙扣的平均数比乙组的平均数少一个.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 1-2$\sqrt{2}$ | D. | 1-$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
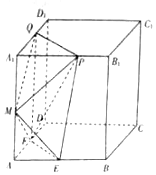 如图,正方体ABCD-A1B1C1D1中,E、F,M分别是AB,AM,AA1的中点,P,Q分别是A1B1,A1D1上的动点(不与A1重合),且A1P=A1Q.
如图,正方体ABCD-A1B1C1D1中,E、F,M分别是AB,AM,AA1的中点,P,Q分别是A1B1,A1D1上的动点(不与A1重合),且A1P=A1Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PD⊥AB,平面PAB⊥平面ABCD,点E,F为棱PB,PC中点,二面角F-AD-C的平面角的余弦值为$\frac{3\sqrt{13}}{13}$.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PD⊥AB,平面PAB⊥平面ABCD,点E,F为棱PB,PC中点,二面角F-AD-C的平面角的余弦值为$\frac{3\sqrt{13}}{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com