练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱柱ABCA1B1C1中，AB AC，点E，F分别在棱BB1，CC1上（均异于端点），且∠ABE∠ACF，AE⊥BB1，AF⊥CC1．

    求证：（1）平面AEF⊥平面BB1C1C；

    （2）BC //平面AEF．

    【答案】(1)证明见解析；(2)证明见解析.

    【解析】试题分析：（1）在三棱柱中， // ，由可推出，再根据，可证平面，从而可证平面平面；（2）根据， ， ， ，可证≌，结合（1），可推出四边形是平行四边形，即可证明//平面．

    试题解析：证明：（1）在三棱柱中， // ．

    ∵

    ∴

    又∵， ， ， 平面.

    ∴平面

    又∵ 平面

    ∴平面平面

    （2）∵， ， ，

    ∴≌

    ∴

    又由（1）知， ．

    ∴四边形是平行四边形，从而 ．

    又∵ 平面， 平面

    ∴//平面．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若是的一个极值点，求的最大值；

    （2）若， ，都有 ，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数, ．

    （Ⅰ）设，求函数的单调区间；

    （Ⅱ）若，函数，试判断是否存在，使得为函数的极小值点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点P为曲线C上任意一点， ，直线、的斜率之积为．

    （Ⅰ）求曲线的轨迹方程；；

    （Ⅱ）是否存在过点的直线与椭圆交于不同的两点、，使得？若存在，求出直线的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据消费者心理学的研究，商品的销售件数与购买人数存在一定的关系，商家可以根据此调整相应的商品小手策略，以谋求商品更多销量，从而获取更多利润.某商场对购买人数和销售件数进行了统计对比，得到如下表格：

    人数

    10

    15

    20

    25

    30

    35

    40

    件数

    4

    7

    12

    15

    20

    23

    27

    （参考公式：，）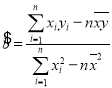

    （1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图：

    （2）根据（1）中所绘制的散点图，可得出购买人数与商品销售件数存在怎样的关系？并求出回归直线方程；（结果保留到小数点后两位）

    （3）预测当进店人数为80人时，商品销售的件数.（结果保留整数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，以轴为始边做两个锐角，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为

    （1）求的值； （2）求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，AE垂直于平面，，，点F为平面ABC内一点，记直线EF与平面BCE所成角为，直线EF与平面ABC所成角为．

    Ⅰ求证：平面ACE；

    Ⅱ若，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）在圆内直径所对的圆周角是直角.此定理在椭圆内（以焦点在轴上的标准形式为例）可表述为“过椭圆的中心的直线交椭圆于两点，点是椭圆上异于的任意一点，当直线，斜率存在时，它们之积为定值.”试求此定值；

    （2）在圆内垂直于弦的直径平分弦.类比（1）将此定理推广至椭圆，不要求证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某登山队在山脚处测得山顶的仰角为，沿倾斜角为（其中）的斜坡前进后到达处，休息后继续行驶到达山顶．

    （1）求山的高度；

    （2）现山顶处有一塔．从到的登山途中，队员在点处测得塔的视角为．若点处高度为，则为何值时，视角最大？

    查看答案和解析>>

    同步练习册答案