
【题目】如图,在三棱锥V-ABC中,平面VAB![]() 平面ABC,
平面ABC,![]() VAB为等比三角形,AC
VAB为等比三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分别为AB,VA的中点。
,O,M分别为AB,VA的中点。
(I)求证:VB//平面MOC;
(II)求证:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱锥V-ABC的体积。
【答案】(I)证明详见解析;(II)证明详见解析;(III)![]()
【解析】
(I)因为O,M分别为AB,VA的中点,
所以OM//VB
又因为VB![]() 平面MOC
平面MOC
所以VB//平面MOC
(II)因为AC=BC,O为AB的中点,
所以OC![]() AB
AB
又因为平面VAB![]() 平面ABC,且OC
平面ABC,且OC![]() 平面ABC,
平面ABC,
所以OC![]() 平面VAB。
平面VAB。
(III)在等腰直角三角形ACB中,AC=BC=![]() ,
,
所以AB=2,OC=1.
所以等边三角形VAB的面积![]() .
.
又因为CO![]() 平面VAB,
平面VAB,
所以三棱锥C-VAB的体积等于![]() .
.
又因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,
所以三棱锥V-ABC的体积为![]() 。
。
【考点精析】通过灵活运用向量语言表述线面的垂直、平行关系,掌握要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线![]() 的方向向量是
的方向向量是![]() ,平面
,平面![]() 内的两个相交向量分别为
内的两个相交向量分别为![]() ,若
,若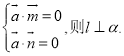 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图,椭圆E:![]() (a>b>0)经过点A(0,-1),且离心率为
(a>b>0)经过点A(0,-1),且离心率为![]() .
.
(1)求椭圆E的方程;
(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P-ABC中,PA![]() 平面ABC,
平面ABC,![]()

(1)(Ⅰ)求三棱锥P-ABC的体积;
(2)(Ⅱ)证明:在线段PC上存在点M,使得AC![]() BM,并求
BM,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若n是一个三位正整数,且n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(1)写出所有个位数字是5的“三位递增数” ;
(2)若甲参加活动,求甲得分X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额
某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额
(单位:万元)都在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
(Ⅰ)直方图中的![]() ;
;
(Ⅱ)在这些购物者中,消费金额在区间![]() 内的购物者的人数为 .
内的购物者的人数为 . 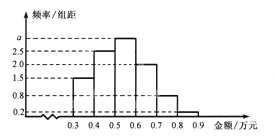
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com