练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    棱长为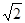的正四面体的外接球半径为     ．

    解析试题分析：记正四面体棱长为，外接球半径为，在正四面体中，利用棱，与棱共顶点的高及这条棱在对面上的射影构成的直角三角形可解得，因此中本题中.
    考点：正四面体（正棱锥的性质）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    将棱长为2的正方体切割后得一几何体，其三视图如图所示，则该几何体的体积为___________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    一个三棱锥的正视图和侧视图及其尺寸如图所示（均为直角三角形），则该三棱锥的俯视图的面积为      .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知圆柱M的底面直径与高均等于球O的直径，则圆柱M与球O的体积之比
    =     ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    [2014·苏州模拟]长和宽分别相等的两个矩形如图所示．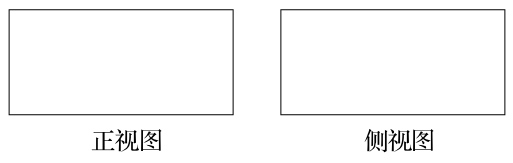

    给定下列四个命题：
    ①存在三棱柱，其正视图、侧视图如图；
    ②存在四棱柱，其俯视图与其中一个视图完全一样；
    ③存在圆柱，其正视图、侧视图如图；
    ④若矩形的长与宽分别是2和1，则该几何体的最大体积为4.
    其中真命题的序号是________(写出所有真命题的序号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等，这时圆柱、圆锥、球的体积之比为          .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    空间中任意放置的棱长为2的正四面体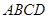.下列命题正确的是_________.（写出所有正确的命题的编号）
    ①正四面体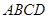的主视图面积可能是；
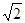    ②正四面体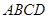的主视图面积可能是；
    ③正四面体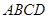的主视图面积可能是；
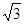    ④正四面体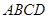的主视图面积可能是2
    ⑤正四面体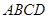的主视图面积可能是.

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    一简单组合体的三视图及尺寸如右图所示（单位: ）则该组合体的体积为（  ）

    A．60000B．64000C．70000D．72000

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图，一个封闭的三棱柱容器中盛有水，且侧棱长AA1＝8．若侧面AA1B1B水平放置时，液面恰好经过AC，BC，A1C1，B1C1的中点． 当底面ABC水平放置时，液面高度为________．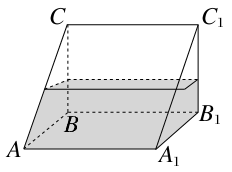

    查看答案和解析>>

    同步练习册答案