
分析 (1)利用an=Sn-Sn-1求出通项公式,根据通项公式判断.
(2)根据an的通项公式判断an的符号变化,然后对n的范围进行讨论求和.
解答 解:(1)当n=1时,a1=S1=99,当n≥2时,an=Sn-Sn-1=100n-n2-[100(n-1)-(n-1)2]=101-2n,显然当n=1时,an=101-2n也成立.
∴an=101-2n,∴an+1-an=101-2(n+1)-(101-2n)=-2.
∴{an}是等差数列,a1=99,d=-2.
(2)令an≥0,得101-2n≥0,解得n≤50.∴当n≤50时,bn=an,当n≥51时,bn=-an.
设数列{bn}的前n项和为Tn,
∴当n≤50时,Tn=Sn=100n-n2,
当n≥51时,Tn=S50-a51-a52-…-an=S50-(Sn-S50)=2S50-Sn=2(100×50-502)-(100n-n2)=n2-100n+5000.
点评 本题考查了等差数列的判断,数列求和,判断出an的符号变化是关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
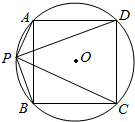 已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.
已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d1+d2=$\frac{4\sqrt{5}}{5}$ | B. | d1•d2=$\frac{4\sqrt{5}}{5}$ | C. | d1+d2=$\frac{4}{5}$ | D. | d1•d2=$\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com