
【题目】设函数f(x)=x2+2ax﹣b2+4
(1)若a是从0,1,2三个数中任取的一个数,b是从﹣2,﹣1,0,1,2五个数中任取的一个数,求函数f(x)有零点的概率;
(2)若a是从区间[﹣3,3]上任取的一个数,b是从区间[0,3]上任取的一个数,求函数g(x)=f(x)+5无零点的概率.
【答案】
(1)解:函数f(x)=x2+2ax﹣b2+4有零点等价于方程x2+2ax﹣b2+4=0有实根,
可得△=(2a)2﹣4(﹣b2+4)≥0,可得a2+b2≥4
记事件A为函数f(x)=x2+2ax﹣b2+4有零点,
总的基本事件共有15个:(0,﹣2,),(2,﹣1),(2,﹣2),(0,﹣1),
(1,﹣1),(1,﹣2),(0,0),(0,1),(0,2),(1,0),(1,1),
(1,2),(2,0),(2,1),(2,2),事件A包含9个基本事件,
∴P(A)= ![]()
(2)解:如图,试验的全部结果所构成的区域为(矩形区域)

函数g(x)=f(x)+5无零点表示事件A,所构成的区域为A={(a,b)|a2+b2<9且(a,b)∈Ω}即图中的阴影部分.
∴P(A)= ![]() .
.
【解析】(1)问题等价于a2+b2≥4,列举可得基本事件共有15个,事件A包含6个基本事件,可得概率;(2)作出图形,由几何概型的概率公式可得.
【考点精析】本题主要考查了几何概型的相关知识点,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】已知直线l:y=2x+m与圆O:x2+y2=1相交于A,B两个不同的点,且A(cosα,sinα),B(cosβ,sinβ).
(1)当△AOB面积最大时,求m的取值,并求出|AB|的长度.
(2)判断sin(α+β)是否为定值;若是,求出定值的大小;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足an+2SnSn﹣1=0(n≥2),a1= ![]() .
.
(1)求证:{ ![]() }是等差数列;
}是等差数列;
(2)求an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时),飞机先看到山顶的俯角为15°,经过420s(秒)后又看到山顶的俯角为45°,求山顶的海拔高度(取 ![]() ,
, ![]() ).
). 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,D,E分别是BC,AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P﹣BC﹣A的平面角为γ,则α,β,γ的大小关系是( ) 
A.α<β<γ
B.α<γ<β
C.β<α<γ
D.γ<β<α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(1,2)
=(1,2)
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ.
的夹角θ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,D为AB的中点.
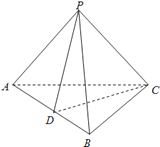
(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com