已知关于x的方程|x2-2x-3|-a=0,该方程实数解的个数有如下判断:
①若该方程没有实数根,则a<-4
②若a=0,则该方程恰有两个实数解
③该方程不可能有三个不同的实数根
④若该方程恰有三个不同的实数解,则a=4
⑤若该方程恰有四个不同的实数解,则0<a<4
其中正确判断的序号是________.
②④⑤
分析:将方程|x
2-2x-3|-a=0的实数解的个数问题转化为函数图象的交点问题,作图分析即得答案.
解答:
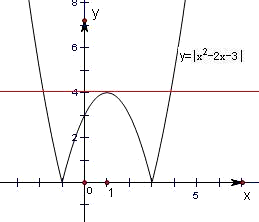
解:关于x的方程|x
2-2x-3|-a=0,即|x
2-2x-3|=a,
分别画出y=|x
2-2x-3|与y=a的图象,如图.
①若该方程没有实数根,则a<0;故①错;
②若a=0,则该方程恰有两个实数解;②对;
③若a=4时,该方程有三个不同的实数根,故③错;
④若该方程恰有三个不同的实数解,则a=4,④对;
⑤若该方程恰有四个不同的实数解,则0<a<4,正确.
其中正确判断的序号是 ②④⑤.
故答案为:②④⑤.
点评:本题考查了根的存在性及根的个数判断.华罗庚曾说过:“数缺形时少直观,形缺数时难入微.数形结合百般好,隔离分家万事非.”数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.

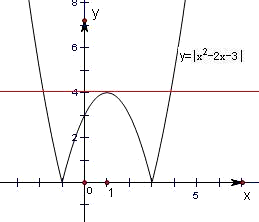 解:关于x的方程|x2-2x-3|-a=0,即|x2-2x-3|=a,
解:关于x的方程|x2-2x-3|-a=0,即|x2-2x-3|=a,
