
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点. 
(1)求证:MN∥BC;
(2)若M,N分别为PB,PC的中点,
①求证:PB⊥DN;
②求二面角P﹣DN﹣A的余弦值.
【答案】
(1)证明:因为底面ABCD为直角梯形,所以BC∥AD.
因为BC平面ADNM,AD平面ADNM,
所以BC∥平面ADNM.
因为BC平面PBC,平面PBC∩平面ADNM=MN,
所以MN∥BC.
(2)解:①因为M,N分别为PB,PC的中点,PA=AB,
所以PB⊥MA.
因为∠BAD=90°,所以DA⊥AB.
因为PA⊥底面ABCD,所以DA⊥PA.
因为PA∩AB=A,所以DA⊥平面PAB.所以PB⊥DA.
因为AM∩DA=A,所以PB⊥平面ADNM,
因为DN平面ADNM,所以PB⊥DN.
解:②如图,以A为坐标原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系A﹣xyz.
则A(0,0,0),B(2,0,0),C(2,1,0),D(0,2,0),P(0,0,2).
由(2)知,PB⊥平面ADNM,所以平面ADNM的法向量为 ![]() =(﹣2,0,2).
=(﹣2,0,2).
设平面PDN的法向量为 ![]() =(x,y,z),
=(x,y,z),
因为 ![]() ,
, ![]() ,
,
所以 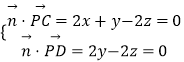 .
.
令z=2,则y=2,x=1.所以 ![]() =(1,2,2),
=(1,2,2),
所以cos< ![]() >=
>= 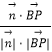 =
= ![]() =
= ![]() .
.
所以二面角P﹣DN﹣A的余弦值为 ![]()

【解析】(1)推导出BC∥AD,从而BC∥平面ADNM,由此能证明MN∥BC.(2)①推导出PB⊥MA,DA⊥AB,从而DA⊥PA.再由PB⊥DA,得PB⊥平面ADNM,由此能证明PB⊥DN.②以A为坐标原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系A﹣xyz利用向量法能求出二面角P﹣DN﹣A的余弦值.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:
①四边形MENF为平行四边形;
②若四边形MENF面积s=f(x),x∈(0,1),则f(x)有最小值;
③若四棱锥A﹣MENF的体积V=p(x),x∈(0,1),则p(x)为常函数;
④若多面体ABCD﹣MENF的体积V=h(x),x∈( ![]() ,1),则h(x)为单调函数;
,1),则h(x)为单调函数;
其中假命题为 ( )
A.①
B.②
C.③
D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(x+a)(x﹣a+3),g(x)=2x+2﹣1,若对任意x∈R,f(x)>0和g(x)>0至少有一个成立,则实数a的取值范围是( )
A.(1,2)
B.(2,3)
C.(﹣2,﹣1)∪(1,+∞)
D.(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,AD‖BC,且 ![]() ,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设
,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设 ![]() (M与C不重合).
(M与C不重合). 
(1)求证:CD⊥DP;
(2)若PA∥平面BME,求k的值;
(3)若二面角M﹣BE﹣A的平面角为150°,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四点A、B、C、D满足| ![]() |=3,|
|=3,| ![]() |=7,|
|=7,| ![]() |=11,|
|=11,| ![]() |=9,则
|=9,则 ![]()
![]() 的取值为( )
的取值为( )
A.只有一个
B.有二个
C.有四个
D.有无穷多个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+2|x﹣a|,x∈R.
(1)若函数f(x)为偶函数,求实数a的值;
(2)当x=﹣1时,函数f(x)在x=﹣1取得最大值,求实数a的取值范围.
(3)若函数f(x)有三个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题正确的是( )
A.经过空间中的三点,有且只有一个平面
B.空间中,如果两个角的两条边分别对应平行,那么这两个角相等
C.空间中,两条异面直线所成角的范围是(0, ![]() ]
]
D.如果直线l平行于平面α内的无数条直线,则直线l平等于平面α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的左右焦点分别为F1 , F2 , 离心率为
的左右焦点分别为F1 , F2 , 离心率为 ![]() ,过点F1且垂直于x轴的直线被椭圆截得的弦长为
,过点F1且垂直于x轴的直线被椭圆截得的弦长为 ![]() ,直线l:y=kx+m与椭圆交于不同的A,B两点.
,直线l:y=kx+m与椭圆交于不同的A,B两点.
(1)求椭圆C的方程;
(2)若在椭圆C上存在点Q满足: ![]() (O为坐标原点).求实数λ的取值范围.
(O为坐标原点).求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com