
【题目】某公司拟购买一块地皮建休闲公园,如图,从公园入口![]() 沿
沿![]() ,
,![]() 方向修建两条小路,休息亭
方向修建两条小路,休息亭![]() 与入口的距离为
与入口的距离为![]() 米(其中
米(其中![]() 为正常数),过
为正常数),过![]() 修建一条笔直的鹅卵石健身步行带,步行带交两条小路于
修建一条笔直的鹅卵石健身步行带,步行带交两条小路于![]() 、
、![]() 处,已知
处,已知![]() ,
,![]() .
.

(1)设![]() 米,
米,![]() 米,求
米,求![]() 关于
关于![]() 的函数关系式及定义域;
的函数关系式及定义域;
(2)试确定![]() ,
,![]() 的位置,使三条路围成的三角形
的位置,使三条路围成的三角形![]() 地皮购价最低.
地皮购价最低.
【答案】(1) ![]() ,定义域为
,定义域为![]() (2)见解析
(2)见解析
【解析】
(1)法一:由![]() 得
得![]() ,
,![]() ,进而得
,进而得![]() ,得y关于x的函数关系即可;法二:由
,得y关于x的函数关系即可;法二:由![]() 得
得![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() 中,由正弦定理
中,由正弦定理![]() 结合
结合![]() ,求得y关于x的函数关系即可;(2) 设三条路围成地皮购价为
,求得y关于x的函数关系即可;(2) 设三条路围成地皮购价为![]() 元,地皮购价为
元,地皮购价为![]() 元/平方米,则
元/平方米,则![]() (
(![]() 为常数),利用换元法结合基本不等式求
为常数),利用换元法结合基本不等式求![]() =
=![]() 最小值即可
最小值即可
(1)法一:由![]() 得
得![]() ,
,![]()
且![]()
由题可知![]()
所以![]()
得![]()
即![]()
所以![]()
由 得定义域为
得定义域为![]()
法二: 由![]() 得
得![]() ,
,![]()
![]()
设![]()
![]() 中,由正弦定理
中,由正弦定理![]()
所以![]()
同理可得![]()
由![]()
即![]()
整理得![]() ,
,
由 得定义域为
得定义域为![]()
(2)设三条路围成地皮购价为![]() 元,地皮购价为
元,地皮购价为![]() 元/平方米,则
元/平方米,则![]() (
(![]() 为常数),
为常数),
所以要使![]() 最小,只要使
最小,只要使![]() 最小
最小
由题可知![]()
定义域为![]()
令![]()
则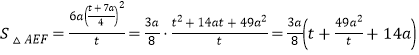
![]()
当且仅当![]() 即
即![]() 时取等号
时取等号
所以,当![]() 时,
时,![]() 最小,所以
最小,所以![]() 最小,此时y=
最小,此时y=![]()
答:当点![]() 距离点
距离点![]()
![]() 米,F距离点
米,F距离点![]() 米远时,三条路围成地皮购价最低
米远时,三条路围成地皮购价最低


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从高三抽出![]() 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
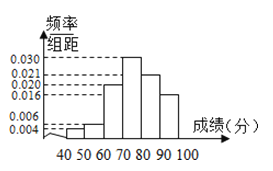
(1)这![]() 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;
(2)这![]() 名学生的平均成绩.
名学生的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点;
至少经过其样本数据点中的一个点;
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强.
之间的负相关很强.
以上正确说法的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和到直线
和到直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点作垂直于
,过点作垂直于![]() 轴的直线与曲线
轴的直线与曲线![]() 相交于两点,直线
相交于两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 相交于一点(交点位于线段
相交于一点(交点位于线段![]() 上,且与
上,且与![]() 不重合).
不重合).
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,四边形
相切时,四边形![]() 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() .
.
(1)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(2)已知![]() ,
,![]() ,若
,若![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值;
的最大值;
(3)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com