
【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第![]() 年与年销量
年与年销量![]() (单位:万件)之间的关系如表:
(单位:万件)之间的关系如表:
| 1 | 2 | 3 | 4 |
| 12 | 28 | 42 | 56 |

(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合![]() 与
与![]() 的回归模型,并用相关系数甲乙说明;
的回归模型,并用相关系数甲乙说明;
(Ⅲ)建立![]() 关于
关于![]() 的回归方程,预测第5年的销售量约为多少?.
的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:  ,
, ![]() ,
, ![]() .
.
参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
科目:高中数学 来源: 题型:
【题目】某气象站观测点记录的连续4天里, ![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位
(单位![]() )的情况如下表1:
)的情况如下表1:
![]()
哈尔滨市某月![]() 指数频数分布如下表2:
指数频数分布如下表2:
![]()
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(参考公式: ![]() ,其中
,其中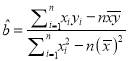 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当![]() 不高于200时,洗车店平均每天亏损约2000元;当
不高于200时,洗车店平均每天亏损约2000元;当![]() 在
在![]() 时,洗车店平均每天收入约4000元;当
时,洗车店平均每天收入约4000元;当![]() 大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】刘徽是我国魏晋时期著名的数学家,他编著的《海岛算经》中有一问题:“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高几何?” 意思是:为了测量海岛高度,立了两根表,高均为5步,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人恰观测到岛峰,从后表退行127步,也恰观测到岛峰,则岛峰的高度为( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙C过点P(1,1),且与⊙M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(1)求⊙C的方程;
(2)设Q为⊙C上的一个动点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱.
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥.
D.棱台各侧棱的延长线交于一点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过点P(﹣2,1),
(1)若直线l与直线x+y﹣1=0平行,求直线l的方程;
(2)若点A(﹣1,﹣2)到直线l的距离为1,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题:
①函数y=tanx的一个对称中心是( ![]() ,0);
,0);
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一条对称轴是x=﹣
)的一条对称轴是x=﹣ ![]() ;
;
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数.
]上是增函数.
写出所有正确的命题的题号 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知θ为向量 ![]() 与
与 ![]() 的夹角,|
的夹角,| ![]() |=2,|
|=2,| ![]() |=1,关于x的一元二次方程x2﹣|
|=1,关于x的一元二次方程x2﹣| ![]() |x+
|x+ ![]()
![]() =0有实根.
=0有实根.
(Ⅰ)求θ的取值范围;
(Ⅱ)在(Ⅰ)的条件下,求函数f(θ)=sin(2θ+ ![]() )的最值及对应的θ的值.
)的最值及对应的θ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com