
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).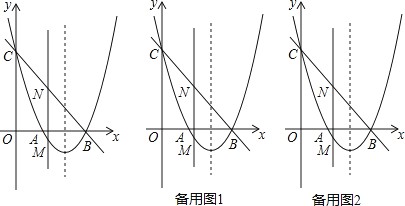
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:将点B(3,0)、C(0,3)代入抛物线y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣4x+3.
(2)
解:设点M的坐标为(m,m2﹣4m+3),设直线BC的解析式为y=kx+3,
把点点B(3,0)代入y=kx+3中,
得:0=3k+3,解得:k=﹣1,
∴直线BC的解析式为y=﹣x+3.
∵MN∥y轴,
∴点N的坐标为(m,﹣m+3).
∵抛物线的解析式为y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为x=2,
∴点(1,0)在抛物线的图象上,
∴1<m<3.
∵线段MN=﹣m+3﹣(m2﹣4m+3)=﹣m2+3m=﹣ ![]() +
+ ![]() ,
,
∴当m= ![]() 时,线段MN取最大值,最大值为
时,线段MN取最大值,最大值为 ![]() .
.
(3)
解:假设存在.设点P的坐标为(2,n).
当m= ![]() 时,点N的坐标为(
时,点N的坐标为( ![]() ,
, ![]() ),
),
∴PB= ![]() =
= ![]() ,PN=
,PN= ![]() ,BN=
,BN= ![]() =
= ![]() .
.
△PBN为等腰三角形分三种情况:
①当PB=PN时,即 ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
此时点P的坐标为(2, ![]() );
);
②当PB=BN时,即 ![]() =
= ![]() ,
,
解得:n=± ![]() ,
,
此时点P的坐标为(2,﹣ ![]() )或(2,
)或(2, ![]() );
);
③当PN=BN时,即 ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
此时点P的坐标为(2, ![]() )或(2,
)或(2, ![]() ).
).
综上可知:在抛物线的对称轴l上存在点P,使△PBN是等腰三角形,点的坐标为(2, ![]() )、(2,﹣
)、(2,﹣ ![]() )、(2,
)、(2, ![]() )、(2,
)、(2, ![]() )或(2,
)或(2, ![]() ).
).
【解析】(1)由点B、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)设出点M的坐标以及直线BC的解析式,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,结合点M的坐标即可得出点N的坐标,由此即可得出线段MN的长度关于m的函数关系式,再结合点M在x轴下方可找出m的取值范围,利用二次函数的性质即可解决最值问题;
(3)假设存在,设出点P的坐标为(2,n),结合(2)的结论可求出点N的坐标,结合点N、B的坐标利用两点间的距离公式求出线段PN、PB、BN的长度,根据等腰三角形的性质分类讨论即可求出n值,从而得出点P的坐标.
【考点精析】掌握二次函数的性质和两点间的距离是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间![]() 内)中,按照5%的比例进行分层抽样,统计结果按
内)中,按照5%的比例进行分层抽样,统计结果按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,整理如下图:
分组,整理如下图:
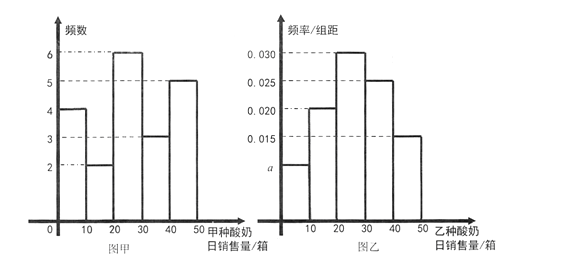
(Ⅰ)写出频率分布直方图(图乙)中![]() 的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为
的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为![]() ,
, ![]() ,试比较
,试比较![]() 与
与![]() 的大小(只需写出结论);
的大小(只需写出结论);
(Ⅱ)从甲种酸奶日销售量在区间![]() 的数据样本中抽取3个,记在
的数据样本中抽取3个,记在![]() 内的数据个数为
内的数据个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)估计1200个日销售量数据中,数据在区间![]() 中的个数.
中的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中, ![]() ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
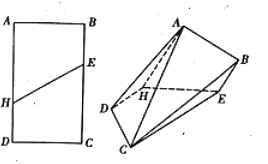
(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() 于
于![]() (不同于点
(不同于点![]() ),延长
),延长![]() 交
交![]() 于
于![]() ,将
,将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,如图
,如图![]() 所示.
所示.
(Ⅰ)若![]() 是
是![]() 的中点,求证:直线
的中点,求证:直线![]() 平面
平面![]() .
.
(Ⅱ)求证: ![]() .
.
(Ⅲ)若平面![]() 平面
平面![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 能否垂直?请说明理由.
能否垂直?请说明理由.
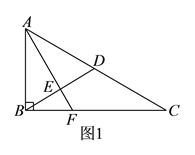
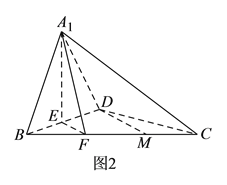
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央电视台为了解该卫视《朗读者》节目的收视情况,抽查东西两部各![]() 个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
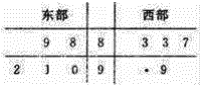
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对朗读以及经典的阅读学习积累的热情,从中获益匪浅,现从观看节目的观众中随机统计了![]() 位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
年龄 |
|
|
|
|
周均学习成语知识时间 |
|
|
|
|
由表中数据,试求线性回归方程![]() ,并预测年龄为
,并预测年龄为![]() 岁观众周均学习阅读经典知识的时间.
岁观众周均学习阅读经典知识的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(![]() )设
)设![]() ,求过点
,求过点![]() 且与圆
且与圆![]() 相切的直线方程.
相切的直线方程.
(![]() )设
)设![]() ,直线
,直线![]() 过点
过点![]() 且被圆
且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
(![]() )设
)设![]() ,直线
,直线![]() 过点
过点![]() ,求
,求![]() 被圆
被圆![]() 截得的线段的最短长度,并求此时
截得的线段的最短长度,并求此时![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com