练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    圆心在原点且圆周被直线3x+4y+15=0分成1：2两部分的圆的方程为     ．
    【答案】分析：圆周被直线分成1：2两部分即∠AOB=×360°=120°，又因为圆心是坐标原点，求出原点到直线的距离，根据在直角三角形中利用30°角所对的直角边等于斜边的一半求出圆的半径，即可得到圆的方程．
    解答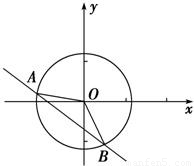：解：如图，因为圆周被直线3x+4y+15=0分成1：2两部分，所以∠AOB=120°．
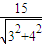
    而圆心到直线3x+4y+15=0的距离d==3，
    在△AOB中，可求得OA=6．所以所求圆的方程为x2+y2=36．
    故答案为：x2+y2=36
    点评：考查学生灵活运用垂径定理解决数学问题，灵活运用点到直线的距离公式化简求值，会根据圆心和半径写出圆的标准方程．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    圆心在原点且圆周被直线3x+4y+15=0分成1：2两部分的圆的方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    圆心在原点且圆周被直线3x+4y+15=0分成1：2两部分的圆的方程为 ________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    圆心在原点且圆周被直线3x+4y+15=0分成1：2两部分的圆的方程为 ______．

    查看答案和解析>>

    科目：高中数学 来源：2011年高三数学第一轮复习巩固与练习：圆的方程（解析版） 题型：解答题

    圆心在原点且圆周被直线3x+4y+15=0分成1：2两部分的圆的方程为     ．

    查看答案和解析>>

    同步练习册答案