
【题目】如图,PA⊥平面ABCD,AD∥BC,AD=2BC,AB⊥BC,点E为PD中点. 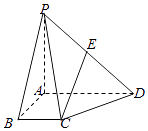
(1)求证:AB⊥PD;
(2)求证:CE∥平面PAB.
【答案】
(1)证明:∵PA⊥平面ABCD,AB平面ABCD,
∴PA⊥AB,
又∵AB⊥BC,AD∥BC,∴AB⊥AD,
又∵PA⊥AB,PA∩AD=A,
∴AB⊥平面PAD,
又PD平面PAD,∴AB⊥PD.
(2)证明:取PA的取中点F,连结EF∥AD,EF= ![]() AD,
AD,
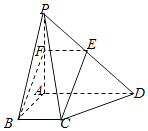
又AD∥BC,AD=2BC,
∴EF∥BC,EF=BC,
∴四边形BCEF是平行四边形,∴EC∥BF,
∵EC平面PAB,BF平面PAB,
∴CE∥平面PAB.
【解析】(1)推导出PA⊥AB,AB⊥AD,由此能证明AB⊥平面PAD,从而AB⊥PD.(2)取PA的取中点F,连结EF∥AD,推导出四边形BCEF是平行四边形,从而EC∥BF,由此能证明CE∥平面PAB.
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的性质是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行.


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点. 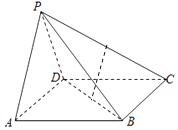
(1)证明:EF∥平面PAD;
(2)证明:直线PA⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 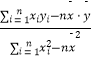 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() .
.
(1)若 ![]() 时,
时, ![]() ,求cos4x的值;
,求cos4x的值;
(2)将 ![]() 的图象向左移
的图象向左移 ![]() ,再将各点横坐标伸长为原来的2倍,纵坐标不变,得y=g(x),若关于g(x)+m=0在区间
,再将各点横坐标伸长为原来的2倍,纵坐标不变,得y=g(x),若关于g(x)+m=0在区间 ![]() 上的有且只有一个实数解,求m的范围.
上的有且只有一个实数解,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在路边安装路灯,路宽为OD,灯柱OB长为h米,灯杆AB长为1米,且灯杆与灯柱成120°角,路灯采用圆锥形灯罩,其轴截面的顶角为2θ,灯罩轴线AC与灯杆AB垂直. 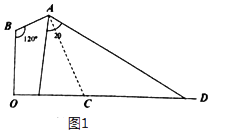
(1)设灯罩轴线与路面的交点为C,若OC=5 ![]() 米,求灯柱OB长;
米,求灯柱OB长;
(2)设h=10米,若灯罩轴截面的两条母线所在直线一条恰好经过点O,另一条与地面的交点为E(如图2); 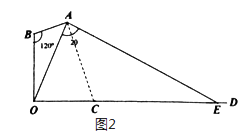
(i)求cosθ的值;
(ii)求该路灯照在路面上的宽度OE的长;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三角形ABC的边长为2,AM是边BC上的高,沿AM将△ABM折起,使得二面角B﹣AM﹣C的大小为90°,此时点M到平面ABC的距离为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是市儿童乐园里一块平行四边形草地ABCD,乐园管理处准备过线段AB上一点E设计一条直线EF(点F在边BC或CD上,不计路的宽度),将该草地分为面积之比为2:1的左、右两部分,分别种植不同的花卉.经测量得AB=18m,BC=10m,∠ABC=120°.设EB=x,EF=y(单位:m). 
(1)当点F与C重合时,试确定点E的位置;
(2)求y关于x的函数关系式;
(3)请确定点E、F的位置,使直路EF长度最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com