
【题目】已知点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() (
(![]() )过点
)过点![]() ,其上顶点为
,其上顶点为![]() ,右顶点和右焦点分别为
,右顶点和右焦点分别为![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),
),![]() ,试判定直线
,试判定直线![]() 是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)直线
(Ⅱ)直线![]() 过定点
过定点![]() .
.
【解析】
(Ⅰ)根据题意得到![]() ,
,![]() 之间的关系式,再结合椭圆的性质,即可求解;
之间的关系式,再结合椭圆的性质,即可求解;
(Ⅱ)先设出直线![]() 的方程,分类讨论,联立直线与椭圆方程,结合韦达定理,分别利用斜率公式化简求值进行计算,得出直线
的方程,分类讨论,联立直线与椭圆方程,结合韦达定理,分别利用斜率公式化简求值进行计算,得出直线![]() 的方程,即可得解.
的方程,即可得解.
(1)因为椭圆![]() :
:![]() (
(![]() )过点
)过点![]() ,所以
,所以![]() .①
.①
又因为![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() .②
.②
把②代入①中,解得![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)直线![]() 过定点.
过定点.
理由如下:当直线![]() 与
与![]() 轴垂直时,设
轴垂直时,设![]() 的方程为
的方程为![]() ,
,
点![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,
所以![]() ,此时直线
,此时直线![]() 过椭圆
过椭圆![]() 的右顶点
的右顶点![]() ,
,
与已知直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点矛盾;
两点矛盾;
当直线![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 的方程为
的方程为![]() ,点
,点![]() ,
,![]() .
.
联立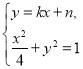 得
得![]() ,
,
则![]() .
.
由韦达定理得![]() ,
,![]() .
.
所以![]()
![]()
![]()
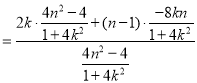
![]() .
.
又因为![]() ,所以
,所以![]() ,
,![]() ,所以存在
,所以存在![]() ,使
,使![]() 成立.
成立.
此时直线![]() 的方程为
的方程为![]() ,即
,即![]() ,所以直线
,所以直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为ρ=2cos θ,直线l的参数方程为![]() (t为参数,α为直线的倾斜角).
(t为参数,α为直线的倾斜角).
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C有唯一的公共点,求角α的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二进制”来源于我国古代的《易经》,该书中有两类最基本的符号:“—”和“——”,其中“—”在二进制中记作“1”,“——”在二进制中记作“0”,例如二进制数![]() 化为十进制的计算如下:
化为十进制的计算如下:![]() .若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
.若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
A.0B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点F的坐标为
右焦点F的坐标为![]() ,点
,点![]() 在椭圆C上,过F且斜率为
在椭圆C上,过F且斜率为![]() 的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
(I)求椭圆C的方程;
(Ⅱ)设线段AB的垂直平分线与x轴、y轴分别相交于点C,D.若![]() 与
与![]() 的面积相等,求直线l的斜率k.
的面积相等,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2013年至2019年新能源汽车y(单位:百台)的数据如下表:

(Ⅰ)求y关于x的线性回归方程,并预测该市2021年新能源汽车台数;
(Ⅱ)该市某公司计划投资600台“双枪同充”(两把充电枪)、“一拖四群充”(四把充电枪)的两种型号的直流充电桩.按要求,充电枪的总把数不少于该市2021年新能源汽车预测台数,若双枪同充、一拖四群充的每把充电枪的日利润分别为25元,10元,问两种型号的充电桩各安装多少台时,才能使日利润最大,求出最大日利润.![]()
附:回归直线的斜率和截距的最小二乘法估计公式分别为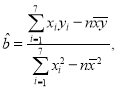
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2019年的高考考生人数是2016年高考考生人数的1.2倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考情况,得到如图柱状图:

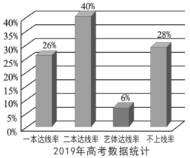
则下列结论正确的是( ).
A.与2016年相比,2019年不上线的人数有所增加
B.与2016年相比,2019年一本达线人数减少
C.与2016年相比,2019年二本达线人数增加了0.3倍
D.2016年与2019年艺体达线人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共
名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共![]() 种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以
种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以![]() 人一组或者
人一组或者![]() 人一组.如果
人一组.如果![]() 人一组,则必须角色相同;如果
人一组,则必须角色相同;如果![]() 人一组,则
人一组,则![]() 人角色相同或者
人角色相同或者![]() 人为级别连续的
人为级别连续的![]() 个不同角色.已知这
个不同角色.已知这![]() 名学生扮演的角色有
名学生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,现在新加入
人,现在新加入![]() 名学生,将这
名学生,将这![]() 名学生分成
名学生分成![]() 组进行游戏,则新加入的学生可以扮演的角色的种数为________.
组进行游戏,则新加入的学生可以扮演的角色的种数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com