
已知双曲线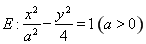 的中心为原点
的中心为原点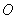 ,左、右焦点分别为
,左、右焦点分别为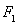 、
、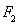 ,离心率为
,离心率为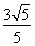 ,点
,点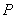 是直线
是直线 上任意一点,点
上任意一点,点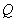 在双曲线
在双曲线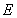 上,且满足
上,且满足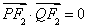 .
.
(1)求实数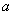 的值;
的值;
(2)证明:直线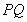 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为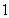 ,过点
,过点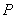 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、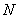 ,在线段
,在线段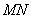 上去异于点
上去异于点 、
、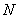 的点
的点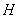 ,满足
,满足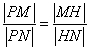 ,证明点
,证明点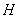 恒在一条定直线上.
恒在一条定直线上.
(1)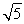 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)根据双曲线的离心率列方程求出实数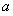 的值;(2)设点
的值;(2)设点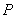 的坐标为
的坐标为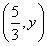 ,点
,点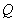 的坐标为
的坐标为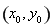 ,利用条件
,利用条件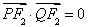 确定
确定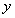 与
与 、
、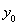 之间的关系,再结合点
之间的关系,再结合点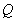 在双曲线
在双曲线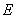 上这一条件,以及斜率公式来证明直线
上这一条件,以及斜率公式来证明直线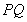 与直线
与直线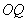 的斜率之积是定值;(3)证法一是先设点
的斜率之积是定值;(3)证法一是先设点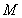 、
、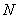 的坐标分别为
的坐标分别为 、
、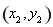 ,结合(2)得到
,结合(2)得到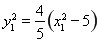 ,
,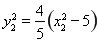 ,引入参数
,引入参数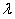 ,利用
,利用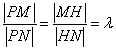 转化为相应的条件
转化为相应的条件 ,利用坐标运算得到点
,利用坐标运算得到点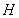 的坐标所满足的关系式
的坐标所满足的关系式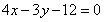 ,进而证明点
,进而证明点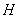 恒在定直线
恒在定直线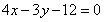 上;证法二是设直线
上;证法二是设直线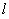 的方程为
的方程为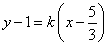 ,将直线
,将直线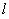 的方程与双曲线的方程联立,结合韦达定理,将条件
的方程与双曲线的方程联立,结合韦达定理,将条件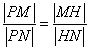 进行等价转化为
进行等价转化为 ,结合韦达定理化简为
,结合韦达定理化简为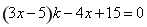 ,最后利用点
,最后利用点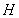 在直线
在直线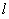 上得到
上得到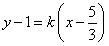 ,从而消去
,从而消去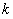 得到
得到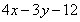
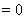 ,进而证明点
,进而证明点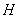 恒在定直线
恒在定直线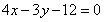 上.
上.
试题解析:(1)根据双曲线的定义可得双曲线的离心率为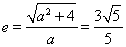 ,由于
,由于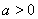 ,解得
,解得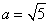 ,
,
故双曲线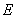 的方程为
的方程为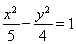 ;
;
(2)设点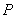 的坐标为
的坐标为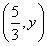 ,点
,点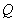 的坐标为
的坐标为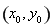 ,易知点
,易知点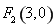 ,
,
则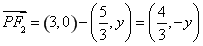 ,
,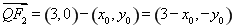 ,
,
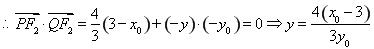 ,因此点
,因此点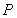 的坐标为
的坐标为 ,
,
故直线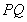 的斜率
的斜率 ,直线
,直线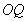 的斜率为
的斜率为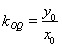 ,
,
因此直线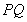 与直线
与直线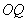 的斜率之积为
的斜率之积为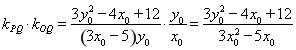 ,
,
由于点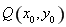 在双曲线
在双曲线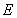 上,所以
上,所以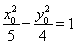 ,所以
,所以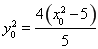 ,
,
于是有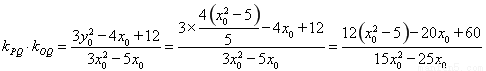
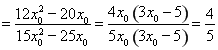 (定值);
(定值);
(3)证法一:设点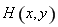 且过点
且过点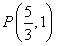 的直线
的直线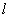 与双曲线
与双曲线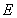 的右支交于不同的两点
的右支交于不同的两点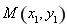 、
、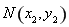 ,由(2)知,
,由(2)知,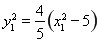 ,
,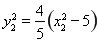 ,
,
设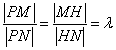 ,则
,则 ,即
,即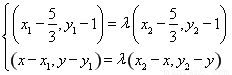 ,
,
整理得 ,
,
由① ③,②
③,② ④得,
④得, ,
,
将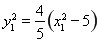 ,
,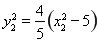 ,代入⑥得
,代入⑥得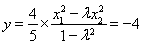 ,⑦,
,⑦,
将⑦代入⑤得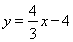 ,即点
,即点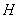 恒在定直线
恒在定直线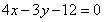 上;
上;
证法二:依题意,直线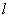 的斜率
的斜率 存在,设直线
存在,设直线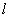 的方程为
的方程为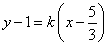 ,
,
由 ,
,
消去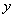 得
得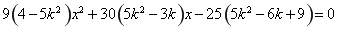 ,
,
因为直线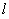 与双曲线
与双曲线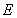 的右支交于不同的两点
的右支交于不同的两点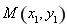 、
、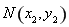 ,
,
则有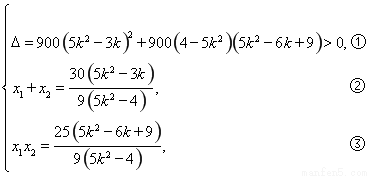 ,
,
设点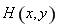 ,由
,由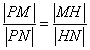 ,得
,得 ,
,
整理得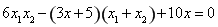 ,
,
将②③代入上式得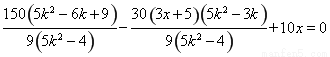 ,
,
整理得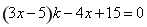 ,④
,④
因为点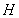 在直线
在直线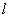 上,所以
上,所以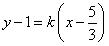 ,⑤
,⑤
联立④⑤消去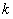 得
得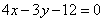 ,所以点
,所以点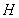 恒在定直线
恒在定直线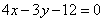 .
.
考点:1.双曲线的离心率;2.向量的坐标运算;3.斜率公式;4.韦达定理


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:选择题
关于线性回归,以下说法错误的是( )
(A)自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
(B)在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图
(C)线性回归直线方程最能代表观测值x,y之间的关系,且其回归直线一定过样本中心点(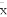 ,
,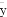 )
)
(D)甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性作试验,并由回归分析法分别求得相关系数rxy如下表
| 甲 | 乙 | 丙 | 丁 |
rxy | 0.82 | 0.78 | 0.69 | 0.85 |
则甲同学的试验结果体现A,B两变量更强的线性相关性
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数 ,
,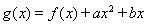 ,函数
,函数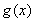 的图象在点
的图象在点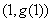 处的切线平行于
处的切线平行于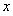 轴.
轴.
(1)确定 与
与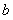 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意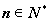 ,都有
,都有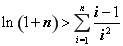 成立。
成立。
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:填空题
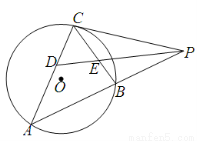
如图,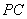 是圆
是圆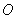 的切线,切点为点
的切线,切点为点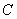 ,直线
,直线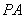 与圆
与圆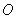 交于
交于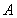 、
、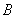 两点,
两点,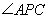 的角平分线交弦
的角平分线交弦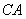 、
、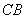 于
于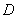 、
、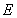 两点,已知
两点,已知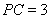 ,
,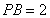 ,则
,则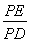 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:选择题
设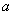 、
、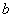 、
、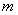 为整数
为整数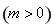 ,若
,若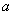 和
和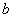 被
被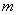 除得余数相同,则称
除得余数相同,则称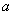 和
和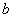 对模
对模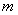 同余,记
同余,记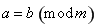 .若
.若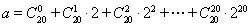 ,且
,且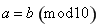 ,则
,则 的值可以为( )
的值可以为( )
A. B.
B.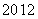 C.
C.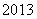 D.
D.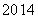
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:填空题
抛物线y=x2上的点到直线x+y+1=0的最短距离为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com