已知函数
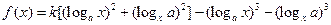
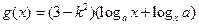
,(其中
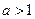
),设
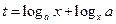
.
(1)当
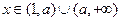
时,试将
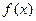
表示成
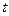
的函数
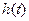
,并探究函数
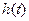
是否有极
值;
(2)当
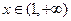
时,若存在
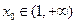
,使
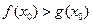
成立,试求
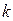
的范围.
(1)
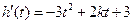
;当
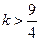
时
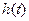
在定义域内有且仅有一个极值,
当
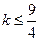
时
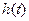
在定义域内无极值;(2)
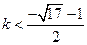
或
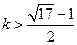
(1)∵
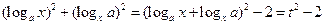
,
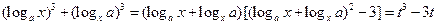
,
∴
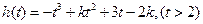
∴
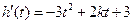
设
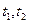
是
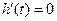
的两根,则
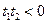
,∴
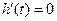
在定义域内至多有一解,
欲使
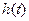
在定义域内有极值,只需
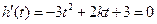
在
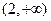
内有解,且
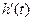
的值在根的左右两侧异号,∴
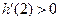
得
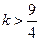
综上:当
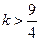
时
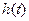
在定义域内有且仅有一个极值,
当
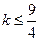
时
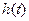
在定义域内无极值
(2)∵存在
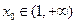
,使
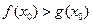
成立等价于
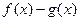
的
最大值大于0
∵
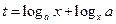
,∴

,
∴
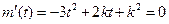
得

.
当
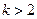
时,
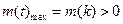
得
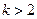
;
当
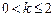
时,
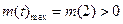
得
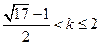
当
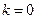
时,
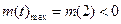
不成立
当
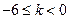
时,
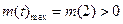
得
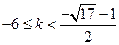
;
当
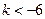
时,
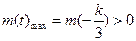
得
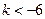
;
综上得:
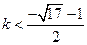
或
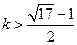
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
设
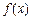
对
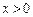
有意义,
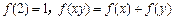
,且
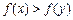
成立的充要条件是
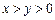
.
(1)求
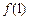
与
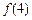
的值;
(2)当
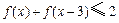
时,求
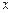
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知定义域为
R上的函数
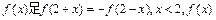
单调递增,如果
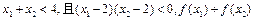
的值
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
定义在R上的函数
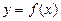
,
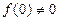
,当
x>0时,
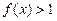
,且对任意的
a、
b∈R,有
f(
a+
b)=
f(
a)·
f(
b).
(1)求证:
f(0)=1;
(2)求证:对任意的
x∈R,恒有
f(
x)>0;
(3)求证:
f(
x)是R上的增函数;
(4)若
f(
x)·
f(2
x-
x2)>1,求
x的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若f(x)=a
x(a>0且a≠1)对于任意实数x、y都有( )
| A.f(xy)=f(x)•(y) | B.f(xy)=f(x)+(y) | C.f(x+y)=f(x)f(y) | D.f(x+y)=f(x)+f(y) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
定义:若存在常数k,使得对定义域D内的任意两个

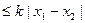
成立,则函数

在定义域D上满足得普希茨条件

。若函数

满足利普希茨条件,则常数k的最小

值为
。

查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
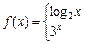
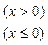
,且关于
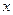
的方程
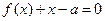
有且仅有两个实根,则实数
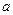
的取值范围是
▲ .
查看答案和解析>>

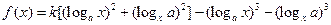
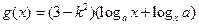 ,(其中
,(其中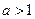 ),设
),设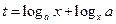 .
.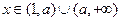 时,试将
时,试将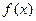 表示成
表示成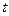 的函数
的函数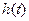 ,并探究函数
,并探究函数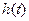 是否有极
是否有极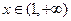 时,若存在
时,若存在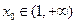 ,使
,使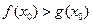 成立,试求
成立,试求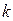 的范围.
的范围. 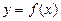 ,
,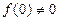 ,当x>0时,
,当x>0时,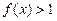 ,且对任意的a、b∈R,有f(a+b)=f(a)·f(b).
,且对任意的a、b∈R,有f(a+b)=f(a)·f(b).